
5.(2006全国Ⅱ)已知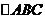 的三个内角A、B、C成等差数列,且AB=1,BC=4,则边BC上的中线AD的长为_________.
的三个内角A、B、C成等差数列,且AB=1,BC=4,则边BC上的中线AD的长为_________.
4. (2006全国Ⅰ)用长度分别为2、3、4、5、6(单位: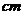 )的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为 ( )
)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为 ( )
A. 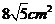 B.
B. 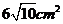 C.
C. 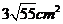 D.
D. 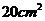
3.(2002年上海)在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是
A.等腰直角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
2.在△ABC中,AB=3,BC=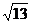 ,AC=4,则边AC上的高为( )
,AC=4,则边AC上的高为( )
A.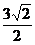 B.
B.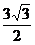 C.
C.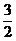 D.
D.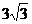
1.(2006山东)在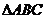 中,角
中,角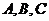 的对边分别为
的对边分别为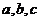 ,已知
,已知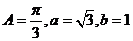 ,则
,则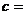 ( )
( )
A.1 B.2 C.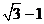 D.
D.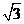
6.熟练掌握实际问题向解斜三角形类型的转化,能在应用题中抽象或构造出三角形,标出已知量、未知量,确定解三角形的方法;提高运用所学知识解决实际问题的能力
5.利用余弦定理,可以解决以下两类问题:
(1)已知三边,求三角;(2)已知两边和它们的夹角,求第三边和其他两角。
4.利用正弦定理,可以解决以下两类问题:
(1)已知两角和任一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求另一边的对角;有三种情况:
bsinA<a<b时有两解;a=bsinA或a=b时有 解;a<bsinA时无解。
3. 余弦定理:a2=b2+c2-2bccosA,
余弦定理:a2=b2+c2-2bccosA, 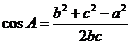 ;
;
证明:如图ΔABC中,
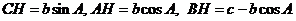
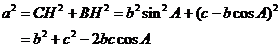
当A、B是钝角时,类似可证。
正弦、余弦定理可用向量方法证明。
要掌握正弦定理、余弦定理及其变形,结合三角公式,能解有关三角形中的问题.
2.正弦定理: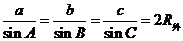
证明:由三角形面积
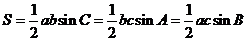
得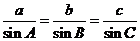
画出三角形的外接圆及直径易得: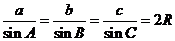
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com