
21.由已知,得B={2,3}.
∵A∩B=A∪B,∴A=B.于是2,3是一元二次方程x2-ax+a2-19=0的两个根,由韦达定理知:
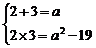 解之,得 a=5.
解之,得 a=5.
20. 由A B
B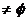 知方程组
知方程组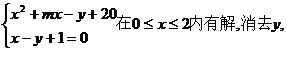
得x2+(m-1)x=0 在0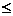 x
x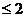 内有解,
内有解,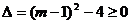 即m
即m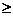 3或m
3或m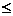 -1。
-1。
若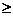 3,则x1+x2=1-m<0,x1x2=1,所以方程只有负根。
3,则x1+x2=1-m<0,x1x2=1,所以方程只有负根。
若m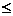 -1,x1+x2=1-m>0,x1x2=1,所以方程有两正根,且两根均为1或两根一个大于1,一个小于1,即至少有一根在[0,2]内。
-1,x1+x2=1-m>0,x1x2=1,所以方程有两正根,且两根均为1或两根一个大于1,一个小于1,即至少有一根在[0,2]内。
因此{m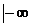 <m
<m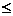 -1}.
-1}.
19. U={1,2,3,4,5} A={1,4}或A={2,3} CuA={2,3,5}或{1,4,5} B={3,4}(CUA)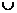 B=(1,3,4,5),又
B=(1,3,4,5),又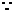 B={3,4}
B={3,4} 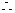 CUA={1,4,5} 故A只有等于集合{2,3},
CUA={1,4,5} 故A只有等于集合{2,3},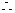 P=-(3+4)=-7 , q=2×3=6.
P=-(3+4)=-7 , q=2×3=6.
18. A={0,-4},又A B=B,所以B
B=B,所以B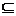 A.
A.
(i)B=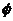 时,
时,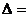 4(a+1)2-4(a2-1)<0,得a<-1;
4(a+1)2-4(a2-1)<0,得a<-1;
(ii)B={0}或B={-4}时,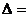 0 得a=-1;
0 得a=-1;
(iii)B={0,-4}, 解得a=1.
解得a=1.
综上所述实数a=1 或a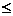 -1.
-1.
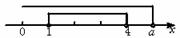
17. 将数集A表示在数轴上(如图),要满足A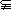 B,表示数a的点必须在4或4的右边,所求a的取值集合为{a|a≥4}.
B,表示数a的点必须在4或4的右边,所求a的取值集合为{a|a≥4}.
16.(1)(A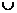 B)
B)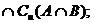 (2)[(CUA)
(2)[(CUA)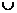 (CUB)]
(CUB)]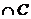 ;
;
(3)(A B)
B) (CUC).
(CUC).
15. 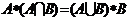 ;
;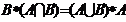 ;
;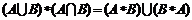 ;….
;….
14.  .
.
13. 16.
1.C 2.D 3.C 4.B 5.C 6.B 7.D 8.A 9.C 10.C 11.A 12.D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com