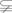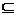19．(本题满分12分)已知三个集合A={x|x²-3x+2=0},B={x|x²-ax+(a-1)=0},C={x|x²-bx+2=0},问同时满足B A、CA的实数a、b是否存在?若存在,求出a、b所有值的集合;若不存在,请说明理由.

解:∵A={x|x²-3x+2=0}={1,2},

又B 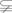A,∴B={1}或B={2}或B=.

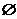又B={x|x²-ax+(a-1)=0}={x|(x-1)［x-(a-1)］=0},

∴B={1},即a-1=1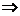a=2.

由B=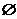,得(-a)²-4(a-1)<0,

即(a-2)²<0.

∴a无解.

由C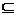A,得b²-8<0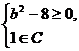或或

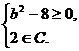
解得b=3.

综上所述,a=2,b=3.

18．(本小题满分12分)(1)已知A={1,x,y},B={x,x²,xy}且A=B,求x、y;

(2)设集合P={4,3t+2,5t²},Q={3t-2,5t-6,5t²-1},且P∩Q={4},求实数t及P∪Q.

(1)解法一:由集合元素的互异性知x≠y,x≠1,y≠1.

∵A=B,∴x²=1或xy=1.

(1)x²=1时,取x=-1,此时A={1,-1,y},B={-1,1,-y}.

由A=B,有y=-y,从而y=0.

(2)xy=1时,即x=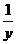,此时A={1, 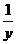,y},B={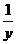,　,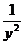1}.

由A=B,有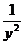=y,从而y=1,但与y≠1矛盾,应舍去.

综上知x=-1,y=0.

解法二:∵A=B,

∴

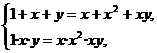
即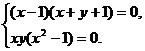

由集合元素的互异性,有x≠1,x≠0.

∴

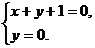
∴x=-1,y=0.

(2)解:①令3t-2=4,则t=2,此时P={4,8,10},而Q中的元素3t-2,5t-6,皆为4,与元素的互异性矛盾,应舍去t=2.

②令5t-6=4,则t=2,显然不符合要求.

③令5t²-1=4,则t=±1.

当t=1时,集合P中的3t+2与5t²皆为5,与元素的互异性矛盾,应舍去t=1;

当t=-1时,P={4,-1,5},Q={-5,-11,4},满足P∩Q={4}.

综上知t=-1.

17．(本小题满分10分)已知集合A={x|x²-3x+2=0},B={x|x²-ax+3a-5=0}.若A∩B=B，求实数a的取值范围.

解:A={x|x²-3x+2=0}={1,2},

由x²-ax+3a-5=0，知Δ=a²-4(3a-5)=a²-12a+20=(a-2)(a-10).

(1)当2＜a＜10时，Δ＜0,B=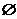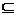A;

(2)当a≤2或a≥10时，Δ≥0，则B≠.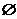

若x=1，则1-a+3a-5=0,得a=2,

此时B={x|x²-2x+1=0}={1}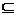A;

若x=2，则4-2a+3a-5=0，得a=1,

此时B={2,-1}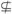A.

综上所述，当2≤a＜10时，均有A∩B=B.

16．(本小题满分10分) 已知A={x|x²-ax+a²-19=0},B={x|x²-5x+8=2},C={x|x²+2x-8=0}.若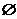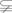A∩B,且A∩C=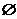,求a的值.

解:∵B={x|(x-3)(x-2)=0}={3,2},

C={x|(x+4)(x-2)=0}={-4,2},

又∵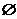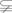A∩B,

∴A∩B≠.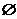

又∵A∩C=,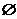

∴-4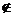A,2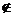A,3∈A.

∴由9-3a+a²-19=0，

解得a=5或a=-2.

(1)当a=5时，A={2,3}，此时A∩C={2}≠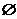,矛盾，

∴a≠5；

(2)当a=-2时，A={-5,3}，此时A∩C=,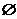

A∩B={3}≠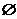,符合条件.

综上(1)(2)知a=-2.

15．(本小题满分10分)已知集合A={2,4,a³-2a²-a+7},B={-4,a+3,a²-2a+2,a³+a²+3a+7},若A∩B={2,5},求实数a的值,并求A∪B.

解:∵A∩B={2,5},

∴5∈A,A={2,4,5},

由已知可得a³-2a²-a+7=5.

∴a³-2a²-a+2=0.

∴(a²-1)(a-2)=0.∴a=2或a=±1.

(1)当a=2时,B={-4,5,2,25},A∩B={2,5}与题设相符;

(2)当a=1时,B={-4,4,1,12},A∩B={4}与题设矛盾;

(3)当a=-1时,B={-4,2,5,4},A∩B={2,4,5}与题设矛盾.

综上(1)、(2)、(3)知a=2,且A∪B={2,4,5}∪{-4,5,2,25}={-4,2,4,5,25}.

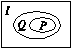
14．设I是全集,非空集合P、Q满足P 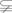　Q 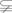I.若含P、Q的一个集合运算表达式,使运算结果为空集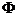,则这个运算表达式可以是　　　　 .(只要求写出一个表达式)

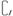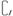答案：Q∩P或Q∩P)等

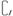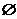解析:由图可知, Q∩P=或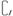Q∩(Q∩P)=.

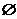13.用描述法表示图中阴影部分的点(包括边界上的点)的坐标的集合应为　　　　 .

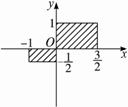
答案:{(x,y)|-1≤x≤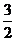,-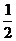≤y≤1,xy≥0}

解析:由阴影部分的点的坐标取值范围可知-1≤x≤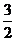,-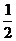≤y≤1.

又由阴影部分的点满足在一、三象限或在坐标轴上,则xy≥0.

12．已知集合M={0,1,2},N={x|x=2a,a∈M},则集合M∩N=　　　　 .

答案:{0,2}

解析:∵M={0,1,2},N={x|x=2a,a∈M},

∴N={0,2,4}.∴M∩N={0,2}.

11．设集合M={x|x∈Z且62-x∈Z},若用列举法表示集合M,则M=　　　　 .

答案:{-4,-1,0,1,3,4,5,8}

解析:设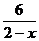=k,k∈Z,则x=.

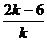令k=±1时,x=-4,x=8;k=±2时,x=-1,x=5;k=±3时,x=0,x=4;k=±6时,x=1,x=3.

10．设M、N是两个非空集合,定义M-N={x|x∈M,且x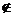N},则M-(M-N)等于()

A.M∪N　　　 B.M∩N　　　 C.M　　　　 D.N

答案:B

解析:画出韦恩图,如下:

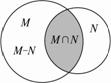
由图可知M-(M-N)=M∩N.故选B.

第Ⅱ卷(非选择题共70分)