
3.一个物体以初速度v0水平抛出,落地时速度为v,那么物体运动时间是( )
A.(v-v0)/g B.(v+v0)/g C.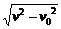 /g D.
/g D.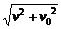 /g
/g
2.关于平抛物体的运动,下列说法中正确的是 ( )
A.平抛物体运动的速度和加速度都随时间的增加而增大
B.平抛物体的运动是变加速运动
C.做平抛运动的物体仅受到重力的作用,所以加速度保持不变
D.做平抛运动的物体水平方向的速度逐渐增大
6.平抛运动的拓展(类平抛运动)
有时物体的运动与平抛运动很相似,也是在某方向物体做匀速直线运动,另一垂直方向做初速度为零的匀加速直线运动。对这种运动,像平抛又不是平抛,通常称作类平抛运动,处理方法与平抛一样,只是a不同而已。
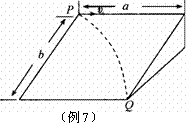 例7 如图所示,光滑斜面长为a,宽为b,倾角为θ,一物块沿斜面左上方顶点P水平射入,而从右下方顶点Q离开斜面,求入射初速度。
例7 如图所示,光滑斜面长为a,宽为b,倾角为θ,一物块沿斜面左上方顶点P水平射入,而从右下方顶点Q离开斜面,求入射初速度。
解析 物块在垂直于斜面方向没有运动,物块沿斜面方向上的曲线运动可分解为水平方向上初速度v0的匀速直线运动和沿斜面向下初速度为零的匀加速运动.
在沿斜面方向上mgsinθ = ma加 a加=gsinθ………①,
水平方向上的位移s = a = v0t ②
沿斜面向下的位移y = b =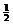 a加t2 ③ 由①②③得v0=a·
a加t2 ③ 由①②③得v0=a·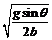
点评 运用运动分解的方法来解决曲线运动问题,就是分析好两个分运动,根据分运动的运动性质,选择合适的运动学公式求解。
[同步检测]
l.关于平抛运动,下列说法中错误的是 ( )
A.是匀变速运动 B.任意两段时间内速度变化方向相同
C.是变加速运动 D.任意两段时间内速度变化大小相等
5.平抛运动的速度变化和一个重要推论
⑴ 水平方向分速度保持vx = v0,竖直方向,加速度恒为g,速度vy = gt,从抛出点起,每隔Δt时间的速度的矢量关系如图5所示,这一矢量关系有两个特点:①任意时刻的速度水平分量均等于初速度v0; ②任意相等时间间隔Δt内的速度改变量均竖直向下,且Δv=Δvy=gΔt。
 ⑵ 平抛物体任意时刻瞬时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。
⑵ 平抛物体任意时刻瞬时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。
证明 设时间t内物体的水平位移为s,竖直位移为h,如图6,则末速度的水平分量vx=v0=s/t,而竖直分量vy=2h/t, 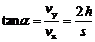 ,所以有
,所以有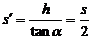
例5 作平抛运动的物体,在落地前的最后1s内,其速度方向由跟竖直方向成600角变为跟竖直方向成450角,求:物体抛出时的速度和高度分别是多少?
解析1 设平抛运动的初速度为v0,运动时间为t,则经过(t-1)s时,vy=g(t一1), tan300=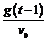
经过ts时:vy=gt,tan450=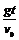 ,∴
,∴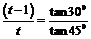 ,
,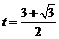 s ;
s ;
∴v0=gt/tan450=23.2 m/s,H=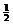 gt2=27.5 m.
gt2=27.5 m.
解析2 此题如果用结论解题更简单.
Δv=gΔt=9. 8m/s,又有v0cot450一v0cot600=Δv,解得v0=23. 2 m/s,
由题可知,落地前瞬间vy= v0 ,所以H=vy2/2g=27.5 m
点评 此题如果画出最后1s初、末速度的矢量图,做起来更直观。
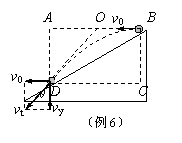 例6 从倾角为θ=30°的斜面顶端以初动能E=6J向下坡方向平抛出一个小球,则小球落到斜面上时的动能E /为______J。
例6 从倾角为θ=30°的斜面顶端以初动能E=6J向下坡方向平抛出一个小球,则小球落到斜面上时的动能E /为______J。
解析 以抛出点和落地点连线为对角线画出矩形ABCD,可以证明末速度vt的反向延长线必然交AB于其中点O,由图中可知AD/AO = 2AD/AB = 2tanθ/1
= 2∶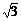 ,由相似形可知vt∶v0=
,由相似形可知vt∶v0=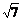 ∶
∶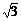 ,因此很容易可以得出结论:E /=14J。
,因此很容易可以得出结论:E /=14J。
4.对平抛运动几个物理量的讨论
(1)平抛运动的物体在空中运动的时间,由抛出点到地面(或者考察点)的高度决定t=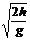 ,与平抛物体的初速度大小无关。
,与平抛物体的初速度大小无关。
(2)平抛物体的水平位移由水平速度和下落高度共同决定,即x=v0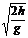 ,在下落高度一定的情况下,水平位移与平抛的初速度成正比。
,在下落高度一定的情况下,水平位移与平抛的初速度成正比。
(3)落地瞬时速度的大小v =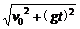 =
=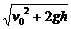 ,由水平初速度v0及高度h决定。
,由水平初速度v0及高度h决定。
(4)落地瞬时速度与水平方向夹角tanθ=gt/v0,h越大,在空中运动时间就越长,θ越大。
(5)落地速度与水平方向夹角θ与位移方向和水平方向夹角α是不相等的,注意不要混淆。
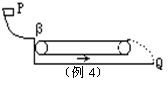
例4 物块从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带以后落到地面上的Q点,若传送带的皮带轮沿逆时针方向转动起来,使传送带随之运动,如图所示,再把物块放到P点自由滑下则( )
 A.物块将仍落在Q点
A.物块将仍落在Q点
B.物块将会落在Q点的左边
C.物块将会落在Q点的右边
D.物块有可能落不到地面上6
解析 物块从斜面滑下来,当传送带静止时,在水平方向受到与运动方向相反的摩擦力,物块将做匀减速运动,离开传送带时做平抛运动。当传送带逆时针转动时物体相对传送带都是向前运动,受到滑动摩擦力方向仍与运动方向相反,物体仍做匀减速运动,离开传送带时,也仍做平抛运动,且与传送带不动时的抛出速度相同,故落在Q点,所以A选项正确。
 思考 若此题中传送带顺时针转动,情况又如何呢?
思考 若此题中传送带顺时针转动,情况又如何呢?
3.斜抛运动的规律
斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的竖直上抛或竖直下抛运动的合运动.
如图3所示,斜上抛物体初速度为v0,与水平方向夹角为θ,则
⑴ 速度公式:
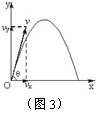 水平速度
水平速度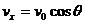 ,竖直速度
,竖直速度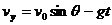
⑵ 位移公式
水平位移x=v0cosθ·t
,竖直位移 y=v0sinθ·t-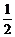 gt2
gt2
 由上两式可得:y=xtanθ-
由上两式可得:y=xtanθ-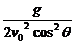 x2
x2
这就是斜抛物体的轨迹方程,由上式可以看出:y=0时,x=0是抛出点位置;x=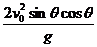 是水平射程,并由此式可知,当θ=45°时,水平射程最大。
是水平射程,并由此式可知,当θ=45°时,水平射程最大。
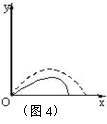
思考 物体在空气中运动时,速度越大,阻力也越大,所以,研究炮弹的运动时就不能忽略空气的阻力,炮弹运动的实际轨迹大致是怎样的?
炮弹在飞行时,由于空气阻力的影响,其运动轨迹不是抛物线,而是一种“弹道曲线”。曲线上升的一段较长而平伸,下降的一段短而弯曲,射程与无空气阻力时相比要小,如图4所示。
2.平抛运动的规律
平抛运动可以看成是水平方向的匀速直线运动和竖直方向的自由落体运动的合运动。
如图2所示,以抛出点为原点,取水平方向为x轴,正方向与初速度v0方向相同,竖直方向为y轴,正方向向下,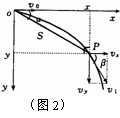 设物体被抛出后,t 秒末,物体的位置为P,其坐标为x(t 秒内的水平位移)和y(t 秒内的下落高度),t 秒末的速度v的坐标分量为vx、vy,则
设物体被抛出后,t 秒末,物体的位置为P,其坐标为x(t 秒内的水平位移)和y(t 秒内的下落高度),t 秒末的速度v的坐标分量为vx、vy,则
⑴ 平抛运动的轨迹
由x=v0t
,
y=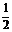 gt2 ,可得y=
gt2 ,可得y=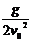 x2,因此平抛运动的轨迹是一条抛物线。
x2,因此平抛运动的轨迹是一条抛物线。
⑵ 位移公式
水平位移x=v0t,竖直位移y=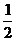 gt2
gt2
平抛物体在t 秒内的位移s,可直接用两个分运动在同一时间内的位移来合成:s=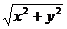 ,位移的方向与水平方向的夹角由下式决定:tanα=
,位移的方向与水平方向的夹角由下式决定:tanα=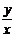 =
=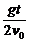
⑶ 速度公式
水平速度为vx=v0 ,竖直速度为 vy=gt
平抛物体在某时刻的瞬时速度用两个分运动在此时刻的瞬时速度来合成,平抛物体在t时刻的速度大小为v =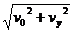 ,速度v的方向与水平方向的夹角β,由下式决定:tanβ=
,速度v的方向与水平方向的夹角β,由下式决定:tanβ=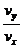 =
=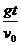
 例1
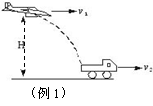
如图所示,飞机距离地面高H=500 m,水平飞行速度为v1=100 m/s,追击一辆速度为v2=20 m/s同向行驶的汽车,欲使投弹击中汽车,飞机应在距汽车水平距离多远处投弹?(g=10 m/s2)
例1
如图所示,飞机距离地面高H=500 m,水平飞行速度为v1=100 m/s,追击一辆速度为v2=20 m/s同向行驶的汽车,欲使投弹击中汽车,飞机应在距汽车水平距离多远处投弹?(g=10 m/s2)
解析
炸弹脱离飞机后做平抛运动,其下落时间由竖直高度决定,即H=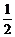 gt2,所以t=
gt2,所以t=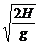 =
=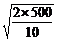 s=10 s。设飞机距车水平距离为x处投弹,则炸弹做平抛运动的水平位移为v1t,在炸弹飞行过程中汽车做匀速运动,其位移为v2t,据几何关系有:x+v2t=v1t
s=10 s。设飞机距车水平距离为x处投弹,则炸弹做平抛运动的水平位移为v1t,在炸弹飞行过程中汽车做匀速运动,其位移为v2t,据几何关系有:x+v2t=v1t
所以x=(v1-v2)t=(100-20)×10 m=800 m.
点评 本题可看作是追及问题的一种变形,在水平方向仍然存在着位移关系:追上时,追及者的位移大小等于被追及者的位移大小与两者初始间距的和.
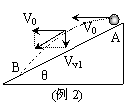 例2 如图在倾角为θ的斜面顶端A处以速度v0水平抛出一小球,落在斜面上的某一点B处,设空气阻力不计,求
例2 如图在倾角为θ的斜面顶端A处以速度v0水平抛出一小球,落在斜面上的某一点B处,设空气阻力不计,求
⑴ 小球从A运动到B处所需的时间;
⑵ 从抛出开始计时,经过多长时间小球离斜面的距离达到最大?
解析 ⑴ 小球做平抛运动,同时受到斜面体的限制,设小球从A运动到B处所需的时间为t,则:水平位移为x=v0t , 竖直位移为y=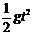 ;
;
由数学关系得到: 
⑵ 从抛出开始计时,经过t1时间,当小球的速度与斜面平行时,小球离斜面的距离达到最大。
因为vy1=gt1=v0tanθ,所以 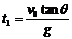
点评 用运动合成和分解方法研究平抛运动,要根据运动的独立性理解平抛运动的两分运动,即水平方向的匀速直线运动和竖直方向的自由落体运动,其运动规律有两部分:一部分是速度规律,另一部分是位移规律。对具体的平抛运动,关键是分析出问题是与位移规律有关还是与速度规律有关。
例3 如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以V0=5m/s的速度在平面上向右运动。求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2)。
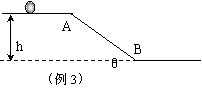 某同学对此题的解法为:小球沿斜面运动,则
某同学对此题的解法为:小球沿斜面运动,则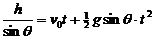 ,由此可求得落地的时间t。问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果。
,由此可求得落地的时间t。问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果。
解析 不同意。小球应在A点离开平面做平抛运动,而不是沿斜面下滑。
正确做法为:落地点与A点的水平距离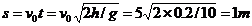
斜面底宽 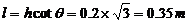
因为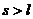 ,所以小球离开A点后不会落到斜面,因此落地时间即为平抛运动时间。
,所以小球离开A点后不会落到斜面,因此落地时间即为平抛运动时间。
∴ 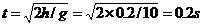
1.关于抛体运动
⑴ 定义:物体以一定的初速度抛出,且只在重力作用下的运动。
⑵ 运动性质:
① 竖直上抛和竖直下抛运动是直线运动;平抛、斜抛是曲线运动,其轨迹是抛物线;
② 抛体运动的加速度是重力加速度,抛体运动是匀变速运动;
③ 抛体运动是一种理想化运动:地球表面附近,重力的大小和方向认为不变,不考虑空气阻力,且抛出速度远小于宇宙速度。
⑶ 处理方法:是将其分解为两个简单的直线运动
 ① 最常用的分解方法是:水平方向上匀速直线运动;竖直方向上自由落体运动或竖直上抛、竖直下抛运动。
① 最常用的分解方法是:水平方向上匀速直线运动;竖直方向上自由落体运动或竖直上抛、竖直下抛运动。
② 在任意方向上分解:有正交分解和非正交分解两种情况,无论怎样分解,都必须把运动的独立性和力的独立作用原理相结合进行系统分解,即将初速度、受力情况、加速度及位移等进行相应分解,如图1所示。
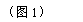 在x方向:以初速度为vx0=v0cosα,
加速度为ax=gsinα的匀加速直线运动。
在x方向:以初速度为vx0=v0cosα,
加速度为ax=gsinα的匀加速直线运动。
在y方向:以初速度为vy0=v0sinα, 加速度为ay=gcosα的匀加速直线运动。
4.为了便于研究初速度为v的平抛运动物体的位置随时间变化的规律,应该沿什么方向建立坐标系?规定什么方向为坐标轴的正方向?应以哪个位置作为坐标原点?
[同步导学]
3.如果物体抛出时速度v不沿水平方向,而是_________或__________的,这种情况称__________,它的受力情况与平抛完全相同,即在水平方向上____________,加速度为________;在竖直方向上_______________,加速度为________。设抛出时速度v与水平方向夹角为θ,则水平方向和竖直方向的初速度v0x = ___________ ,v0y = ___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com