
7.如图所示,某船在河中向东匀速直线航行,船上的人正相对于船以0.4m/s的速度匀速地竖直向上升起一面旗帜,当他用20s升旗完毕时,船行驶了9m,那么旗相对于岸的速度大小是多少?
6.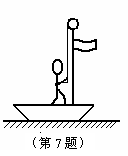 两个相互垂直的运动,一个是匀速,另一个是初速度为零的匀加速运动,其合运动一定是________(填“直线运动”或“曲线运动”)
两个相互垂直的运动,一个是匀速,另一个是初速度为零的匀加速运动,其合运动一定是________(填“直线运动”或“曲线运动”)
5.一人站在匀速运动的自动扶梯上,经时间20s到楼上,若自动扶梯不动,人沿扶梯匀速上楼需要时间30s,当自动扶梯匀速运动的同时,人沿扶梯匀速(相对扶梯的速度不变)上楼,则人到达楼上所需的时间为________s
4.一个物体的运动由水平的匀加速度a1=4m/s2和竖直的匀加速度a2=3m/s2两个分运动组成,关于这个物体的运动加速度说法正确的是( )
A.加速度的数值在1-7m/s2之间 B.加速度的值为5m/s2
C.加速度数值为7m/s2 D.加速度数值为lm/s2
3.一船以恒定的速率渡河,水流速度恒定(小于船速),要使船垂直到达对岸,则( )
A.船应垂直河岸航行
B.船的航行方向应偏向上游一侧
C.船不可能沿直线到达对岸
D.河的宽度一定时,船到对岸的时间是任意的
2.如果两个不在同一直线上的分运动都是匀速直线运动,对其合运动的描述中,正确的是 ( )
A.合运动一定是曲线运动
B.合运动一定是直线运动
C.合运动是曲线运动或直线运动
D.当两个分运动的速度数值相等时,合运动才为直线运动
1.一人游泳渡河以垂直河岸不变的速度(相对水)向对岸游去,河水流动速度恒定.下列说法中正确的是 ( )
A.河水流动速度对人渡河无任何影响
B.游泳渡河的路线与河岸垂直
C.由于河水流动的影响,人到达对岸的时间与静水中不同
D.由于河水流动的影响,人到达对岸的位置,向下游方向偏移
4.连带运动问题
 指物拉绳(杆)或绳(杆)拉物问题。由于高中研究的绳都是不可伸长的,杆都是不可伸长和压缩的,即绳或杆的长度不会改变,所以解题原则是:把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相同求解。
指物拉绳(杆)或绳(杆)拉物问题。由于高中研究的绳都是不可伸长的,杆都是不可伸长和压缩的,即绳或杆的长度不会改变,所以解题原则是:把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相同求解。
例6 如图所示,车甲以速度v1拉车乙前进,乙的速度为v2,甲、乙都在水平面上运动,求v1∶v2
解法1 甲、乙沿绳的速度分别为v1和v2cosα,两者应该相等,所以有v1∶v2=cosα∶1
 解法2
取OB=OC,Δt→0 则∠CBA=900 AC=AB/cosα
解法2
取OB=OC,Δt→0 则∠CBA=900 AC=AB/cosα
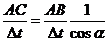
v1= v2cosα
评析 本题关键在于分清乙车运动速度v2是合运动的速度,沿绳方向是分运动速度。
例7 光滑的杆互相垂直地固定在一起,上面分别穿有一个小球,小球a、b间用一细直棒相连,如图。当细直棒与竖直杆夹角为α时,求两小球实际速度之比va∶vb?
 解析 a、b沿杆的分速度分别为vacosα和vbsinα
解析 a、b沿杆的分速度分别为vacosα和vbsinα
∵vacosα= vbsinα
∴va∶vb= tanα∶1
[同步检测]
3.小船渡河问题
一条宽度为L的河,水流速度为Vs,已知船在静水中的航速为Vc,船过河时,船的实际运动(即相对于河岸的运动)可以看成是随水以速度Vs漂流的运动和以Vc相对于静水的划行运动的合运动。随水漂流和划行这两个分运动互不干扰而具有等时性。
 (1)怎样渡河时间最短?
(1)怎样渡河时间最短?
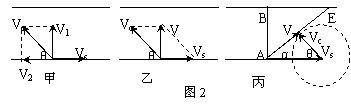
如图2-甲所示,设船头斜向上游与河岸成任意角θ,这时船速在垂直于河岸方向的速度分量V1=Vcsinθ,渡河所需时间为: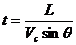
可以看出:L、Vc一定时,t随sinθ增大而减小;当θ=900时,sinθ=1,所以,当船头与河岸垂直时,渡河时间最短,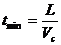 .
.
(2)若Vs<Vc,怎样渡河位移最小?
如图2-乙所示,渡河的最小位移即河的宽度。为了使渡河位移等于L,必须使船的合速度V的方向与河岸垂直。这是船头应指向河的上游,并与河岸成一定的角度θ。根据三角函数关系有:Vccosθ─Vs=0.
所以θ=arccos(Vs/Vc),因为0≤cosθ≤1,所以只有在Vc>Vs时,船才有可能垂直于河岸横渡。
(3)若Vs>Vc,怎样渡河位移最短?
如果水流速度大于船在静水中的航行速度,则不论船的航向如何,总是被水冲向下游。怎样才能使船的位移最短呢?如图2-丙所示,设船头Vc与河岸成θ角,合速度V与河岸成α角。可以看出:α角越大,船的位移越短,那么,在什么条件下α角最大呢?以Vs的矢尖为圆心,以Vc为半径画圆,当v与圆相切时,α角最大,根据cosθ=Vc/Vs,船头与河岸的夹角应为:θ=arccos(Vc/Vs)
此时渡河的最短位移为: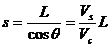
思考:过河的最短时间和最短位移分别决定于什么?
例5 河宽d=100m ,水流速度为v1=4m/s,船在静水中的速度是v2=3m/s,求:
⑴ 欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移是多大?
⑵ 欲使船航行距离最短,船应怎样渡河?渡河时间多长?
解析: 设想水不流动,则船将以v1速度做匀速直线运动,设想船不开行,则船将以v2速度顺水飘流,可见实际渡河时,渡船同时参与两个分运动,其合运动沿v1与 v2矢量和的方向做匀速直线运动,由于分运动与合运动的等时性,船渡河时间等于v1分运动的时间。
 ⑴ 不论v1与v2的大小如何,船头v1的方向垂直指向河岸时,时间最短,
⑴ 不论v1与v2的大小如何,船头v1的方向垂直指向河岸时,时间最短,
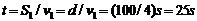
⑵ 因船速小于水速,故小船不能垂直过河,但有无最短航程呢?
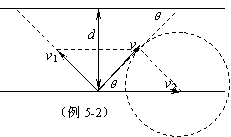 虽然不能垂直过河,但有最短的路程,用画圆的方法可找出最短船程时夹角θ,并可找到这时速度之间关系满足的特征,如图。
虽然不能垂直过河,但有最短的路程,用画圆的方法可找出最短船程时夹角θ,并可找到这时速度之间关系满足的特征,如图。
则sinθ=v1/v2
S=d/sinθ , t=s/v合=d/(sinθ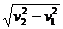 )
)
点评
⑴
不论v1与v2的大小如何,当船头v1的方向垂直指向河岸时,时间最短,且最短时间为
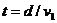 。
。
⑵
当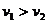 时,合速度垂直过岸,航程最短为d
,当
时,合速度垂直过岸,航程最短为d
,当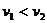 时不能垂直过岸,但仍有最短路程,此时船的实际航向与下游夹θ角,且sinθ=v1/v2 。
时不能垂直过岸,但仍有最短路程,此时船的实际航向与下游夹θ角,且sinθ=v1/v2 。
2.决定合运动的性质和轨迹的因素
物体运动的性质由加速度决定(加速度为零时物体静止或做匀速运动;加速度恒定时物体做匀变速运动;加速度变化时物体做变加速运动)。
 物体运动的轨迹(直线还是曲线)则由物体的速度和加速度的方向关系决定(速度与加速度方向在同一条直线上时物体做直线运动;速度和加速度方向成角度时物体做曲线运动)。
物体运动的轨迹(直线还是曲线)则由物体的速度和加速度的方向关系决定(速度与加速度方向在同一条直线上时物体做直线运动;速度和加速度方向成角度时物体做曲线运动)。
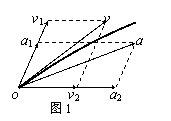
两个互成角度的直线运动的合运动是直线运动还是曲线运动?
决定于它们的合速度和合加速度方向是否共线(如图1所示)。
常见的类型有:
⑴ a=0:匀速直线运动或静止。
⑵ a恒定:性质为匀变速运动,分为:① v、a同向,匀加速直线运动;②v、a反向,匀减速直线运动;③ v、a成角度,匀变速曲线运动(轨迹在v、a之间,和速度v的方向相切,方向逐渐向a的方向接近,但不可能达到。)
 ⑶ a变化:性质为变加速运动,加速度大小、方向都随时间变化。
⑶ a变化:性质为变加速运动,加速度大小、方向都随时间变化。
例4 如图所示的塔吊臂上有一可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩,在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时,吊钩将物体B向上吊起,A、B之间的距离以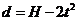 (SI)(SI表示国际单位制,式中H为吊臂离地面的高度)规律变化,则物体做( )
(SI)(SI表示国际单位制,式中H为吊臂离地面的高度)规律变化,则物体做( )
A.速度大小不变的曲线运动.
B.速度大小增加的曲线运动.
C.加速度大小方向均不变的曲线运动.
D.加速度大小方向均变化的曲线运动.
解析 根据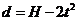 可知,物体在竖直方向上做匀加速直线运动,水平方向为匀速直线运动,合加速度方向与合初速度的方向必不共线,物体做曲线运动,且加速度恒定为匀变速曲线运动,加速度方向与速度方向夹锐角,速度不断增大,所以答案为 B C。
可知,物体在竖直方向上做匀加速直线运动,水平方向为匀速直线运动,合加速度方向与合初速度的方向必不共线,物体做曲线运动,且加速度恒定为匀变速曲线运动,加速度方向与速度方向夹锐角,速度不断增大,所以答案为 B C。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com