
6.物体沿光滑斜面匀减速上滑,加速度大小为4 m/s2,6 s后又返回原出发点.那么下述结论正确的是( ).
A.物体开始沿斜面上滑时速度为12 m/s
B.物体开始沿斜面上滑时速度是10 m/s
C.物体沿斜面上滑的最大位移是18 m
D.物体沿斜面上滑的最大位移是15 m
5.汽车以20m/s的速度做匀速直线运动,刹车后的加速度为5m/s2,那么刹车后2S与刹车后6S汽车通过的位移之比为( )
A.1∶1 B.3∶1 C.3∶4 D.4∶3
4.有一个物体开始时静止在O点,先使它向东作匀加速直线运动,经过5秒钟,使它的加速度方向立即改为向西,加速度的大小不改变,再经过5秒钟,又使它加速度方向改为向东,但加速度大小不改变,如此重复共历时20秒,则这段时间内( )
A.物体运动方向时而向东时而向西 B.物体最后静止在O点
C.物体运动时快时慢,一直向东运动 D.物体速度一直在增大
3.一物体做匀变速直线运动,某时刻速度大小为4m/s,1s后速度大小为10m/s,在这1s内该物体的( )
A.位移的大小可能小于4m B.位移的大小可能大于10m
C.加速度的大小可能小于4m/s2 D.加速度的大小可能大于10m/s2
2.匀变速直线运动的物体,初速度为10 m/s,方向沿x轴正方向,经过2 s,末速度变为10 m/s,方向沿x轴负方向,则其加速度和2 s内的平均速度分别是( ).
A.10 m/s2;0 B.0;10 m/s
C.-10 m/s2;0 D.-10 m/s2;10 m/s
1.物体做匀加速直线运动,如果它的加速度为2 m/s2,那么它在任何1 s内的( )
A.末速度一定比初速度大2 m/s
B.后1 s的位移总比前l s的位移大2 m
C.后1 s的位移总是前1 s的位移的2倍
D.以上结论都不对
2.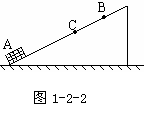 如图1-2-2所示的光滑斜面上,一物体以4m/s的初速度由斜面底端的A点匀减速滑上斜面,途经C和B,C为AB中点,已知vA∶vC= 4∶3,从C点到B点历时(
如图1-2-2所示的光滑斜面上,一物体以4m/s的初速度由斜面底端的A点匀减速滑上斜面,途经C和B,C为AB中点,已知vA∶vC= 4∶3,从C点到B点历时(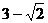 )S,试求:
)S,试求:
(1)到达B点的速度?
(2)AB长度?
1.物体从静止开始作匀加速直线运动,第3 s内通过的位移是3 m,则 ( )
A.第3 s内的平均速度是3 m/s
B.物体的加速度是1.2 m/s2
C.前3 s内的位移是6 m
D.3 s末的速度是3.6 m/s
例1 升降机从静止开始上升,先做匀加速运动,经过4s速度达到4m/s,然后匀速上升2s,最后3s做匀减速运动直到停止,求升降机上升的总高度。
[解析]升降机运动的全过程由三个不同的运动阶段组成:
第一阶段:升降机做初速度为零的匀加速运动;初速度v0 = 0,运动时间t1 = 4 s,末速度v1=4m/s
第二阶段:升降机做匀速运动,速度:v2 = v1 = 4 m/s,运动时间t2 = 2 s
第三阶段:升降机做匀减速运动,初速度v3 = v2 = 4 m/s,运动时间t3 = 3 s且末速度vt = 0
分段求和:
第一阶段:由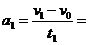 1 m/s2
1 m/s2
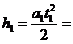 8 m
8 m
第二阶段: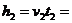 8 m
8 m
第三阶段:由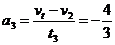 m/s2
m/s2 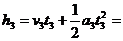 6 m
6 m
上升的总高度h = h1 + h2 + h3 = 22 m
[点评]有关匀变速直线运动的问题,一般解法较多。本题的解法属于规范的基本解法;这类问题物体的运动过程较多,解题的关健是弄清物体的运动过程,再分过程求解。
例2 物体沿某一方向做匀变速直线运动,在时间t内内通过的路程为s,它在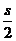 处的速度为
处的速度为 ,在中间时刻的速度为
,在中间时刻的速度为 .则
.则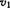 和
和 的关系是 ( )
的关系是 ( )
A.当物体做匀加速直线运动时,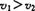
B.当物体做匀减速直线运动时,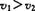
C.当物体做匀速直线运动时,
D.当物体做匀减速直线运动时,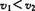
[解析]通过题中的已知量求出用同样的物理量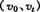 表示的
表示的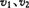 的表达式,这样就可运用数学知识比较
的表达式,这样就可运用数学知识比较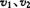 的大小
的大小
设初速度为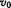 ,末速度为
,末速度为 .由公式
.由公式 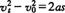 得
得 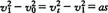
解得 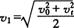
由公式 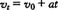 得
得 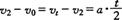
解得 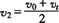
又因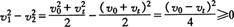 有
有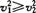
因物体做单方向直线运动,速度总是正值,所以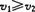 。
。
上式表明物体无论做匀加速直线运动还是做匀减速直线运动,中间位置的速度都大于中间时刻的速度,只有当物体做匀速直线运动时两个速度才相等.所以选项A、B、C都正确.
[点评]由公式 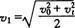 及
及 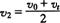 ,运用数学知识:
,运用数学知识: 为2次幂平均值(方均根值),必大于1次幂平均值(算术平均值), 即可得出无论物体做匀加速直线运动,还是做匀减速直线运动,总有
为2次幂平均值(方均根值),必大于1次幂平均值(算术平均值), 即可得出无论物体做匀加速直线运动,还是做匀减速直线运动,总有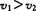 。
。
例3 甲、乙两车从同一地点出发同向运动,其 图像如图1-2-1所示.试计算:
图像如图1-2-1所示.试计算:
(1)从乙车开始运动多少时间后两车相遇?
(2)相遇处距出发点多远?
(3)相遇前两车的最大距离是多少?
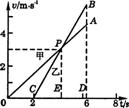
图1-2-1
[解析]从图像知两车初速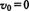 ,加速度分别为:
,加速度分别为: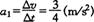

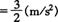 ,做匀加速运动.
,做匀加速运动.
(1)两车相遇位移相等,设乙车运动t秒后两车相遇,则甲、乙两车的位移为
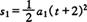
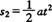
由于
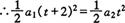 ,代人数据解题
,代人数据解题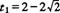 (舍去),
(舍去),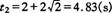
(2)相遇点离出发点的距离为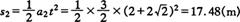
(3)由图知甲车行驶t=4 s时两车速度相等.此时两车距离最大,二者距离为:
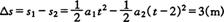
[点评]运动图像能形象、直观地反映物体的运动情况,而且图线的斜率,与t轴所围成的面积等,都有明确的物理意义,因而利用运动图像可以提高解题能力和技巧,甚至可以解决一些用解析法在中学阶段还不能解决的问题.
例4 在火车站站台上有一观察者,在列车开动时恰好站在第一节车厢的最前端,列车起动后做匀加速直线运动;经过4s第一节车厢通过观察者,整个列车经过他历时20s,设每节车厢等长,车厢连接处长度不计,求:
(1)这列列车共有多少节车厢
(2)最后9节车厢通过观察者所经历的时间.
[解析]设每节车厢长度为L,则有
L=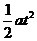 =8a
nL=
=8a
nL=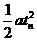 =200a
=200a
解得:n=25节
前16节车厢经过他的时间为 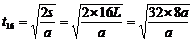 =16s
=16s
故最后9节车厢通过观察者所经历的时间为:20-16=4s
[点评]利用位移求时间,若初速度不为零,列出的一元二次方程求解比较困难,本题求最后9节车厢通过观察者所经历的时间时,为使初速度是零,利用整个列车经过他历时与前16节车厢经过他历时之差就能达到,这类题正确选择研究的过程尤为重要。
例5 质点以加速度a从静止出发做匀加速直线运动,在时刻t加速度变为2a,时刻2t加速度变为3a……,求质点在开始的nt 时间内通过的总位移。
[解析]第一个t时间末,质点的速度和通过的位移为:v1=at 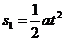
第二个t时间末,质点的速度和通过的位移为:v2 = v1 + 2at = 3at s2=v1t+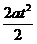 =
=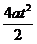
第三个t时间末,质点的速度和通过的位移为:v3 = v2 + 3at = 6at s3 = v2t
+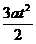 =
=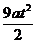
同理:第n个t时间末,质点的速度和通过的位移为: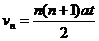
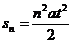
所以质点在时间nt内通过的总位移为
s =
s1+ s2 + s3 + …… sn = (1+22+32+……+n2)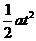
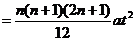
[点评]根据物理条件列出一般数学表达式,分析关系式遵循何种性质的数学规律,找出通项,能很容易地根据数学规律求出物理量。
2.匀变速直线运动的规律
两个基本公式 vt=v0+at
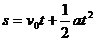
两个推论 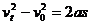
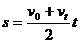
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com