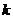10、若过定点且斜率为的直线与圆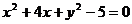在第一象限内的部分有交点，则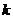的取值范围是(　　 )

A. 　　　B. 　　　C. 　　D.

9、定义在区间(-∞,+∞)的奇函数f(x)为增函数;偶函数g(x)在区间[0,+∞)的图象与f(x)的图象重合,设 a>b>0 ,给出下列不等式:　

　　 　① f(b)-f(-a)>g(a)-g(-b)　 ② f(b)-f(-a)<g(a)-g(-b)

　　 ③ f(a)-f(-b)>g(b)-g(-a)　 ④f(a)-f(-b)<g(b)-g(-a)

其中成立的是　 (　　　 )

(A)①与④　　　 (B)②与③　　 (C)①与③　　　 (D)②与④ 　　

8、在正n棱锥中，相邻两侧面所成的二面角的取值范围是(　 )

(A)(π，π)　　　　　　　　 (B)(π，π)　　　

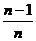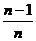(C)(0，)　　　　　　　　　　　 (D)(π，π)

7、不等式组的解集是(　 )

(A)(0，2)　　 (B)(0，2.5)　　　 (C)(0，)　　 (D)(0，3)

6、在圆x+y＝4上与直线4x+3y－12=0距离最小的点的坐标是(　 )

(A)(，)　　　　　　　　　　　 (B)(，－)　　　

(C)(－，)　　　　　　　　　　　 (D)(－，－)

5、函数y=sin(－2x)+sin2x的最小正周期是(　 )

(A)　　　　 (B) 　　　　　　(C) 2　　　　　 (D) 4

4、若，P=，Q=，R=，则(　 )

(A)RPQ　　　　　　　　　　　　 (B)PQ R　

(C)Q PR 　　　　　　　　　　　(D)P RQ

3、设f(x)是(－∞，∞)是的奇函数，f(x+2)＝－f(x)，当0≤x≤1时，f(x)＝x，则f(7.5)等于(　 )

(A) 0.5　　　　 (B) －0.5　　　　 (C) 1.5　　　　　 (D) －1.5

1、如果，那么等于(　 )

2 已知，那么使成立的充要条件是 (　 )

10.1+log_x3与2log_x2(x＞0且x≠1)的大小.

解：(1+log_x3)－2log_x2=log_x.

当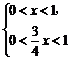或

即0＜x＜1或x＞时，

有log_x＞0，1+log_x3＞2log_x2.

当①或②时，log_x＜0.

解①得无解，解②得1＜x＜，

即当1＜x＜时，有log_x＜0，

1+log_x3＜2log_x2.

当x=1，即x=时，有log_x=0.

∴1+log_x3=2log_x2.

综上所述，当0＜x＜1或x＞时，1+log_x3＞2log_x2；

当1＜x＜时，1+log_x3＜2log_x2；

当x=时，1+log_x3=2log_x2.

　[探索题]x、y是正实数,记

A(x,y)=,B(x,y)=

(1)　　　　 证明:A(x,y)≤B(x,y)

(2)　　　　 是否存在常数C,使得A(x,y)≤C≤B(x,y)恒成立?证明你的结论.

证明:(1)B(x,y)－A(x,y)=

∴A(x,y)≤B(x,y).

(2)鉴于二式中关于x,y的轮换对称性,令x=y,得A(x,y)=B(x,y)=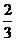

下证A(x,y)≤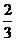≤B(x,y)

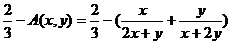
同理.

所以,存在正常数C=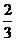,使A(x,y)≤C≤B(x,y)成立.

(2)法2: (放缩法)