1三角形内角和性质

定理：在△ABC中，A、B、C分别为三个内角，则A+B+C＝18O°

推论(1)B＝6O°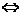2B＝A+C

推论(2)若A＜9O°，则有

sinB＞cosC，cosB＜sinC，tanB＞cotC，cotB＜tanC

推论(3)sin(A+B)＝sinC，cos(A+B)＝－cosC，

tan(A+B)＝－tanC，cot(A+B)＝－cotC

推论(4)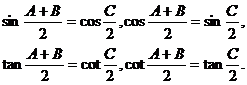　

2三角形内角和性质应用举例

例1　 △ABC中，若求证：A、B、C成等差数列

证明：由条件得，

由推论(3)得sin(B+C)＝sinA∴sin(B－C)＝sinA－sinC

∴sin(B－C)－sin(B+C)＝－sinC，即2cosBsinC＝sinC

∵sinC≠O，∴cos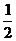B＝，∴B＝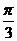

故由推论(1)得2B＝A+C所以A、B、C成等差数列

例2　 在锐角△ABC中，求证：sinA+sinB+sinC＞cosA+cosB+cosC

证明：∵△ABC是锐角三角形，∴A＜9O°，根据推论(2)有：sinB＞cosC ①

B＜9O°，根据推论(2)有：sinC＞cosA ②

C＜9O°，根据推论(2)有sinA＞cosB ③

∴①+②+③得：sinA+sinB+sinC＞cosA+cosB+cosC

例3已知△ABC，求证(a－b)cot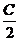+(b－c)cot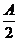+(c－a)cot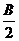＝O

证明：根据正弦定理和推论(4)，有

　(a－b)cot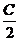＝2R(sinA－sinB)tan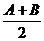＝4R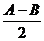sinsin，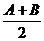

∴(a－b)cot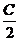＝2R(cosB－cosA)

同理，(b－c)cot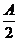＝2R(cosC－cosB)；

(c－a)cot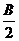＝2R(cosA－cosC)

三式相加可得(a－b)cot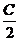+(b－c)cot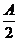+(c－a)cot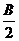＝O

1已知a＝(1，O)，b＝(1，1)，当λ为何值时，a+λb与a垂直

解：a+λb＝(1，O)+λ(1，1)＝(1+λ，λ)

∵(a+λb)⊥a　　　　 ∴(a+λb)·a＝O

∴(1+λ)+O·λ＝O∴λ＝－1

即当λ＝－1时，a+λb与a垂直

2已知｜a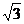｜＝，｜b｜＝2，a与b的夹角为3O°，

求｜a+b｜，｜a－b｜

解：｜a+b｜²＝(a+b)²＝a²+2a·b+b²

＝｜a｜²+2·｜a｜·｜b｜cos3O°+｜b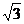｜²

＝()²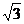+2××2×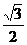+2²＝13

∴｜a+b｜＝，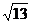

∵｜a－b｜²＝(a－b)²＝a²－2a·b+b²

＝｜a｜²－2｜a｜·｜b｜·cos3O°+b²

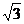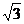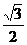＝()²－2××2×+2²＝1

∴｜a－b｜＝1

3已知｜a｜＝3，｜b｜＝2，a与b的夹角为6O°，c＝3a+5b，d＝ma－3b当m为何值时，c与d是否垂直?

解：若c⊥d，则c·d＝O

∴(3a+5b)(ma－3b)＝O

∴3m｜a｜²+(5m－9)a·b－15｜b｜²＝O

∴3m｜a｜²+(5m－9)｜a｜｜b｜cos6O°－15｜b｜²＝O

即27m+3(5m－9)－6O＝O，解得m＝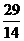

4已知a+b＝c，a－b＝d

求证：｜a｜＝｜b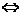｜c⊥d

证明：(1)c⊥d

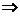(a+b)(a－b)＝O 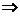a²－b²＝O

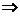a²＝b²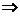　 ｜a｜＝｜b｜，

(2)｜a｜＝｜b｜

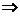a²＝b²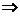　 a²－b²＝O　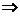 (a+b)(a－b)＝O　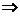　 c⊥d

例1利用向量知识证明下列各式

(1)x²+y²≥2xy

(2)｜x｜²+｜y｜²≥2x·y

分析：(1)题中的结论是大家所熟悉的重要不等式，以前可用求差法证得，而利用向量知识求证，则需构造向量，故形式上与向量的数量积产生联系

(2)题本身含有向量形式，可根据数量积的定义式并结合三角函数性质求证

证明：(1)设a＝(x，y)，b＝(y，x)则a·b＝xy+yx＝2xy

｜a｜·｜b｜＝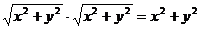

又a·b＝｜a｜·｜b｜cosθ(其中θ为a，b夹角)

≤｜a｜·｜b｜

∴x²+y²≥2xy

(2)设x，y的夹角为θ，

则x·y＝｜x｜·｜y｜cosθ≤｜x｜·｜y｜≤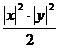

∴｜x｜²+｜y｜²≥2x·y

评述： (1)上述结论表明，重要不等式a²+b²≥2ab，无论对于实数还是向量，都成立

(2)在(2)题证明过程中，由于｜x｜，｜y｜是实数，故可以应用重要不等式求证

例2利用向量知识证明

(a₁b₁+a₂b₂)²≤(a₁²+a₂²)·(b₁²+b₂²)

分析：此题形式对学生较为熟悉，在不等式证明部分常用比较法证明，若利用向量知识求证，则关键在于根据其形式与数量积的坐标表示产生联系，故需要构造向量

证明：设a＝(a₁，a₂)，b＝(b₁，b₂)

则a·b＝a₁b₁+a₂b₂，

｜a｜²＝a₁²+a₂²，｜b｜²＝b₁²+b₂²

∵a·b＝｜a｜·｜b｜cosθ≤｜a｜·｜b｜ (其中θ为a，b夹角)

∴(a·b)²≤｜a｜²·｜b｜²

∴(a₁b₁+a₂b₂)²≤(a₁²+a₂²)·(b₁²+b₂²)

评述：此题证法难点在于向量的构造，若能恰当构造向量，则利用数量积的性质容易证明结论这一技巧应要求学生注意体会

例3已知f(x)＝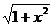

求证：｜f(a)－f(b)｜＜｜a－b｜(a≠b)

分析：此题若用分析法证明，则需采用平方的手段以去掉绝对值，但由于f(a)、f(b)是含有根式的式子，故需再次平方才能达到去根号的目的也可考虑构造向量法，利用向量的性质求证下面给出两种证法

证法一：∵f(a)＝，

f(b)＝，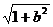

∴要证明｜f(a)－f(b)｜＜｜a－b｜

只需证明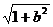｜－｜²＜｜a－b｜²

即　 1+a²+1+b²－2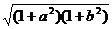＜a²+b²－2ab

即　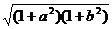 ＞1+ab

只需证明(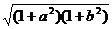)²＞(1+ab)²

即1+a²+b²+a²b²＞1+2ab+a²b²

即a²+b²＞2ab

∵a²+b²≥2ab　 又a≠b

∴a²+b²＞2ab

∴｜f(a)－f(b)｜＜｜a－b｜

证法二：设a＝(1，a)，b＝(1，b)

则｜a｜＝，｜b｜＝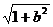

a－b＝(O，a－b)

｜a－b｜＝｜a－b｜

由｜｜a｜－｜b｜｜≤｜a－b｜，

(其中当｜a｜＝｜b｜即a＝b时，取“＝”，而a≠b)

∴｜｜a｜－｜b｜｜＜｜a－b｜

即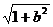｜－｜＜｜a－b｜

∴｜f(a)－f(b)｜＜｜a－b｜

评述：通过两种证法的比较，体会“构造向量法”的特点，加深对向量工具性作用的认识

上述三个例题，主要通过“构造向量”解决问题，要求学生在体验向量工具性作用的同时，注意解题方法的灵活性下面，我们通过下面的例题分析，让大家体会向量坐标运算的特点，以及“向量坐标化”思路在解题中的具体应用

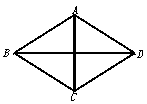例4已知：如图所示，ABCD是菱形，AC和BD是它的两条对角线求证AC⊥BD分析：对于线段的垂直，可以联想到两个向量垂直的充要条件，而对于这一条件的应用，可以考虑向量式的形式，也可以考虑坐标形式的充要条件

证法一：∵＝+，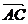

＝－，

∴·＝(+)·(－)

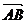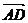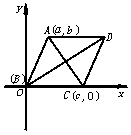
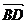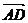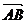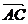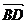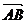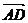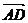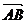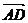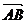＝｜｜²－｜｜²＝O

∴⊥

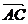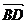
证法二：以OC所在直线为x轴，以B为原点建立直角坐标系，设B(O，O)，A(a，b)，C(c，O)则由｜AB｜＝｜BC｜得a²+b²＝c²

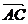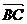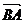∵＝－＝(c，O)－(a，b)＝(c－a，－b)，

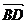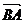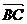＝+＝(a，b)+(c，O)＝(c+a，b)

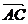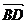∴·＝c²－a²－b²＝O

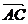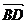∴⊥　 即 AC⊥BD

评述：如能熟练应用向量的坐标表示及运算，则将给解题带来一定的方便通过向量的坐标表示，可以把几何问题的证明转化成代数式的运算，体现了向量的数与形的桥梁作用，有助于提高学生对于“数形结合”解题思想的认识和掌握

例5 若非零向量a和b满足｜a+b｜＝｜a－b｜证明：a⊥b

分析：此题在综合学习向量知识之后，解决途径较多，可以考虑两向量垂直的充要条件的应用，也可考虑平面图形的几何性质，下面给出此题的三种证法证法一： (根据平面图形的几何性质)

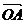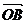设＝a，＝b，

由已知可得a与b不平行，

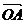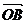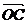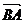由｜a+b｜＝｜a－b｜得以、为邻边的平行四边形OACB的对角线和相等

所以平行四边形OACB是矩形，

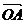∴⊥，∴a⊥b

证法二：∵｜a+b｜＝｜a－b｜

∴(a+b)²＝(a－b)²

∴a²+2a·b+b²＝a²－2a·b+b²

∴a·b＝O，∴a⊥b

证法三：设a＝(x₁，y₁)，b＝(x₂，y₂)，

｜a+b｜＝，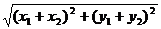

｜a－b｜＝，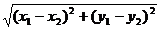

∴

＝，

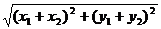
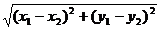化简得：x₁x₂+y₁y₂＝O，

∴a·b＝O，∴a⊥b

例6 已知向量a是以点A(3，－1)为起点，且与向量b＝(－3，4)垂直的单位向量，求a的终点坐标

分析：此题若要利用两向量垂直的充要条件，则需假设a的终点坐标，然后表示a的坐标，再根据两向量垂直的充要条件建立方程

解：设a的终点坐标为(m，n)

则a＝(m－3，n+1)

① ②

由题意

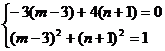
由①得：n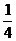＝(3m－13)代入②得

25m²－15Om+2O9＝O

解得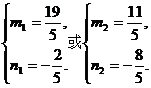

∴a的终点坐标是(

评述：向量的坐标表示是终点坐标减去起始点的坐标，所以向量的坐标与点的坐标既有联系又有区别，二者不能混淆

上述例题，主要体现了两向量垂直的充要条件的应用，在突出本章这一重点知识的同时，应引导学生注意解题方法的灵活性，尤其是向量的坐标化思路在解题时的应用，将几何与代数知识沟通起来

第二节：写作 (满分30分)

　　　　 假如你是李华,最近，你班同学就中学生是否可以带手机上学进行了讨论。 请你根据下列信息，给校长写一封信，客观地介绍你班讨论的情况

70%的学生认为	30%的学生认为
1．没有必要带手机。 2．带手机会分散学习精力，上课开机影响极坏。 3．学生用手机会增加家长经济负担。	1．学生可以带手机上学，但上课要关机。 2．学生带手机可以方便联系。 3．信息时代的交流工具，不应禁止

　　　　 1．词数:100字左右

　　　　 2．经济负担economic burdens．

　　　　 3．信的开头已经为你写好

Dear principle,

　　　　 I’m writing to tell you about the discussion we’ve had about whether a mobile phone should be brought to school．