
6.在平直公路上,汽车由静止做匀加速运动,当速度到达vm后立即关闭发动机直至静止,v-t图象如图16所示,设汽车的牵引力为F,摩擦力为f,全过程中牵引力F做功为W1,摩擦力f对物体做的功为W2,则( )
A.= B.=
C.= D.=
解析:由图象得汽车加速时的加速度大小为
a===
由牛顿第二定律F-f=ma=m
汽车减速时的加速度大小为a′===
由牛顿第二定律f=ma′=m
即F=ma+f=m+m=m
所以=,故选项C对
W1=Fs=m××10=m
W2=fs′=m××40=m,所以选项B对.
答案:BC
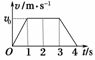
图17
5.如图14所示,DO是水平面,AB是斜面,初速度为v0的物体从D点出发沿DBA滑动到顶点A时速度刚好为零.如果斜面改为AC,让该物体从D点出发沿DCA滑动到A点且速度刚好为零.已知物体与路面之间的动摩擦因数处处相同且不为零,则物体具有的初速度( )
A.大于v0 B.等于v0
C.小于v0 D.取决于斜面的倾斜角

图15
解析:如图15所示,物体由D出发沿DBA路面运动,由动能定理可列出方程:-f1sDB-f2sBA-mghA=0-mv
∵f1=μmg,f2=μmgcosα
代入上式:
-μmgsDB-μmgcosα·sAB-mghA=-mv
又因为sABcosα=sBO
∴μmgsDB+μmgsBO+mghA=mv
则μmg(sDB+sBO)+mghA=mv
μmgsDO+mghA=mv
此式表明由D出发的初速度v0与斜面夹角α无关,因此沿DCA上滑到A点的初速度仍为v0,选项B正确.
答案:B
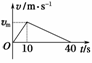
图16
4.如图13所示,质量为m的物块与水平转台之间的动摩擦因数为μ,物体与转动轴相距R,物体随转台由静止开始转动.当转速增加至某值时,物块即将在转台上滑动,此时转台已开始匀速转动,在这一过程中,摩擦力对物体做的功是( )
A.0 B.2μmgR
C.2πμmgR D.μmgR/2
解析:物体由静止到加速到某一速度过程中摩擦力做功.物体的初动能Ek1=0,末动能Ek2=mv2.当物体以速度v与转台一起匀速转动时,摩擦力提供向心力,则μmg=m.据动能定理有Wf=Ek2-Ek1=mv2-0=μmgR.
答案:D
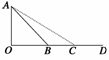
图14
3.(2009年长沙模拟)如图12所示,一物块以6 m/s的初速度从曲面A点下滑,运动到B点速度仍为6 m/s.若物体以5 m/s的初速度仍由A点下滑,则它运动到B点时的速度( )
A.大于5 m/s B.等于5 m/s
C.小于5 m/s D.条件不足,无法计算
解析:物块第一次由A到B,始末位置动能相等,即它从A到B运动过程中重力做的功恰好等于物体克服摩擦力做的功.当物块以5 m/s初速滑到B点时,重力做的功与前次相同.由于速度小,由圆周运动知识知物块在运动过程中对曲面的压力始终小于前次,即物块克服摩擦力做的功比前次少,因而第二次滑动时由A到B重力做的功比物块克服摩擦力做的功多,因而物体的动能一定增加,所以到B时速度一定大于5 m/s.
答案:A
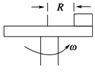
图13
2.一个小物块冲上一个固定的粗糙斜面,经过斜面上A、B两点,到达斜面上最高点后返回时,又通过了B、A两点,如图11所示.关于物块上滑时由A到B的过程和下滑时由B到A的过程,动能的变化量的绝对值ΔE上和ΔE下以及所用时间t上和t下相比较,有( )
A.ΔE上<ΔE下,t上<t下 B.ΔE上>ΔE下,t上>t下
C.ΔE上<ΔE下,t上>t下 D.ΔE上>ΔE下,t上<t下
解析:∵ΔE上=Wf+mgh ΔE下=mgh-Wf
∴ΔE上>ΔE下
∵整个斜面是粗糙的,所以在AB段上>下,
∴t上<t下
答案:D

图12
1.如图9所示,在抗洪救灾中,一架直升机通过绳索,用恒力F竖直向

图9
上拉起一个漂在水面上的木箱,使其由水面开始加速上升到某一高度,若考虑空气阻力而不考虑空气浮力,则在此过程中,以下说法正确的有( )
A.力F所做功减去克服阻力所做的功等于重力势能的增量
B.木箱克服重力所做的功等于重力势能的增量
C.力F、重力、阻力三者合力所做的功等于木箱动能的增量
D.力F和阻力的合力所做的功等于木箱机械能的增量

图10
解析:对木箱受力分析如图10所示,则由动能定理:
WF-mgh-Wf=ΔEk,故C对.
由上式得:WF-Wf=ΔEk+mgh,即WF-Wf=ΔEk+ΔEp=ΔE,故A错,D对.
由重力做功与重力势能变化关系知B对,故B、C、D对.
答案:BCD

图11
22.(本题满分14分)
已知函数 在区间[0,1]上单调递增,在区间[1,2]上单调递减。
在区间[0,1]上单调递增,在区间[1,2]上单调递减。
(1)求a的值;
(2)若斜率为24的直线是曲线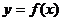 的切线,求此直线方程;
的切线,求此直线方程;
(3)是否存在实数b,使得函数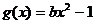 的图象与函数
的图象与函数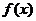 的图象恰有2个不
的图象恰有2个不
同交点?若存在,求出实数b的值;若不存在,试说明理由。
21.(本题满分12分)
已知函数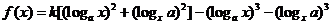 , (其中
, (其中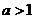 ),
),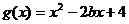 ,设
,设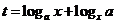 .
.
(Ⅰ)当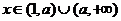 时,将
时,将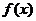 表示成
表示成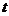 的函数
的函数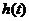 ,并探究函数
,并探究函数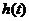 是否有极
是否有极
值;
(Ⅱ)当k=4时,若对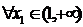 ,
, 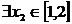 ,使
,使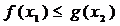 ,试求实数b的取值范围.。
,试求实数b的取值范围.。
20.(本题满分12分)
已知函数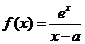 (其中常数
(其中常数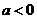 ),
),
(1)求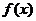 的定义域及单调区间;
的定义域及单调区间;
(2)若存在实数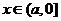 ,使得不等式
,使得不等式 成立,求
成立,求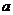 的取值范围.
的取值范围.
19.(本小题满分12分)
某厂生产某种产品的年固定成本为250万元,每生产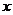 千件,需另投入成本为
千件,需另投入成本为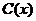 ,
,
当年产量不足80千件时,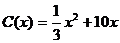 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时, (万元),通过市场分析,若每件售价为500元时,该厂当年生产该产品能全部销售完。
(万元),通过市场分析,若每件售价为500元时,该厂当年生产该产品能全部销售完。
(1)写出年利润 (万元)关于年产量
(万元)关于年产量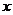 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一产品的生产中所获利润最大,最大利润是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com