
23.(本题满分10分)已知直线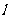 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆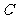 的极坐标方程:
的极坐标方程: (
(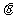 为参数).
为参数).
(1)将直线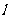 的参数方程和圆
的参数方程和圆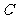 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程; 

(2)判断直线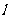 和圆
和圆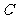 的位置关系.
的位置关系.
22.(本题满分10分)如图,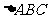 是圆
是圆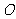 的内接三角形,
的内接三角形, ,D为圆O中弧AB上一点,延长DA至E,使得CE= CD.
,D为圆O中弧AB上一点,延长DA至E,使得CE= CD.
 (1)求证:BD =AE;
(1)求证:BD =AE; 

(2)若AC  BC,求证:AD + BD =
BC,求证:AD + BD =  CD.
CD.
|
22、23两道题中任选一题解答,若两道题都做,则将第22题分数计入总分)
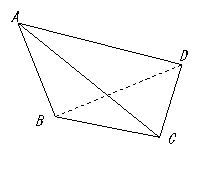
21.(本题满分12分)如图,三棱锥A-BCD中,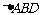 与
与 是全等的直角三角形,AD是公共的斜边,AD=
是全等的直角三角形,AD是公共的斜边,AD= , DB= CD=
, DB= CD=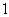 ,另一侧面ABC是正三角形.
,另一侧面ABC是正三角形.
(1)求证:AD BC;
BC;
(2)求二面角B-AC-D的余弦值; 

(3)在线段AC上是否存在一点E,使ED与平面BCD成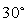 角?若存在,确定点E
角?若存在,确定点E
 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
20.(本题满分12分)设函数 在
在 及
及 时取得极值.
时取得极值.
(1)求a、b的值;
(2)若对于任意的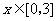 ,都有
,都有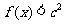 成立,求c的取值范围.
成立,求c的取值范围. 

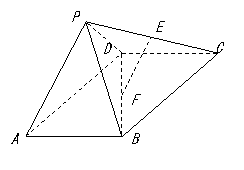
19.(本题满分12分)如图,四棱锥P-ABCD中,ABCD为矩形, 为等腰直角三角形,
为等腰直角三角形, ,平面PAD
,平面PAD  平面ABCD,AB=
平面ABCD,AB=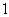 ,AD=
,AD=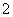 ,E,F分别为PC和BD的中点.
,E,F分别为PC和BD的中点.
 (1)证明:EF//平面PAD;
(1)证明:EF//平面PAD;
(2)求四棱锥P-ABCD的体积. 

18.(本题满分12分) 某工厂生产一种产品,成本C(元)与生产件数x之间的关系为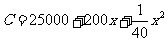 .
. 

(1)要使平均成本最低,应生产多少件产品?
(2)若产品每件500元售出,要使利润最大,应生产多少件产品?
17.(本题满分12分)设P:关于x的不等式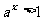 的解集是
的解集是 ,Q:函数
,Q:函数
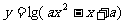 的定义域为R,如果P和Q有且仅有一个正确,求a的取值范围。
的定义域为R,如果P和Q有且仅有一个正确,求a的取值范围。
16.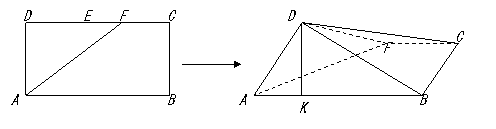 如图,在长方形
如图,在长方形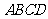 中,
中, ,
,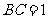 ,
, 为
为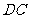 的中点,
的中点,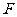 为线段
为线段 (端点除外)上一动点.现将
(端点除外)上一动点.现将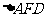 沿
沿 折起,使平面
折起,使平面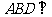 平面
平面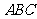 .在平面
.在平面 内过点
内过点 ,作
,作 ,
, 为垂足.设
为垂足.设 ,则
,则 的取值范围是
.
的取值范围是
.
15.设全集 ,若
,若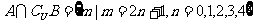 ,
,
则集合B=__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com