
7.复数z=a+bi(a, b R)与复平面上的点 建立了一一对应的关系.
R)与复平面上的点 建立了一一对应的关系.
6.复平面:建立直角坐标系来表示复数的平面叫做复平面, x轴叫做 , 叫虚轴.
5.若z=a+bi, (a, b R), 则 | z |=
; z
R), 则 | z |=
; z =
.
=
.
4.共轭复数:当两个复数实部 ,虚部 时.这两个复数互为共轭复数.(当虚部不为零时,也可说成互为共轭虚数).
3.复数相等:如果两个复数 相等且 相等就说这两个复数相等.
2.分类:设复数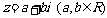 :
:
(1) 当 =0时,z为实数;
(2) 当  0时,z为虚数;
0时,z为虚数;
(3) 当
=0, 且  0时,z为纯虚数.
0时,z为纯虚数.
1.复数:形如
 的数叫做复数,其中a , b分别叫它的
和
.
的数叫做复数,其中a , b分别叫它的
和
.
3、了解复数的代数表示法及其几何意义,能进行复数代数形式的四则运算,了解复数代数形式的加、减运算的几何意义.
|
|
重视复数的概念和运算,注意复数问题实数化.
第1课时 复数的有关概念
|
2、理解复数的基本概念以及复数相等的充要条件
1、了解数系的扩充过程,体会实际需求与数学内部的矛盾(数的运算规则、方程理论)在数系扩充过程中的作用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com