
20. (本小题满分13分)
(本小题满分13分)
 已知向量
已知向量 ,
, ,动点
,动点 到定直线
到定直线 的距离等于
的距离等于 ,并且满足
,并且满足 ,其中
,其中 是坐标原点,
是坐标原点, 是参数。
是参数。
(1)求动点 的轨迹方程;
的轨迹方程;
(2)当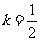 时,若直线
时,若直线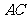 与动点
与动点 的轨迹相交于
的轨迹相交于 、
、 两点,线段
两点,线段 的垂直平分线交
的垂直平分线交 轴
轴 ,求
,求 的取值范围;
的取值范围;
(3)如果动点 的轨迹是一条圆锥曲线,其离心率
的轨迹是一条圆锥曲线,其离心率 满足
满足 ,求
,求 的取值范围。
的取值范围。
19. (本小题满分13分)
(本小题满分13分)
 某出版公司为一本畅销书定价如下:
某出版公司为一本畅销书定价如下: 这里
这里 表示定购书的数量,
表示定购书的数量, 表示定购
表示定购 本所付的钱数(单位:元).
本所付的钱数(单位:元).
 (1)有多少个
(1)有多少个 ,会出现买多于
,会出现买多于 本书比恰好买
本书比恰好买 本书所花钱少?
本书所花钱少?
 (2)若一本书的成本价是5元,现在甲、乙两人来买书,每人至少买1本,甲买的书不多于乙买的书,两人共买60本,问出版公司至少能赚多少钱?最多能赚多少钱?
(2)若一本书的成本价是5元,现在甲、乙两人来买书,每人至少买1本,甲买的书不多于乙买的书,两人共买60本,问出版公司至少能赚多少钱?最多能赚多少钱?
18. (本小题满分12分)
(本小题满分12分)
 如图,在三棱柱
如图,在三棱柱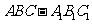 中,
中, 侧面
侧面 ,
,


 为棱
为棱 的中点,已知
的中点,已知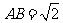 ,
, ,
,

 ,
, ,求:
,求:
 (1)异面直线
(1)异面直线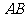 与
与 的距离;
的距离;
 (2)三面角
(2)三面角 的平面角的正切值。
的平面角的正切值。
17. (本小题满分12分)
(本小题满分12分)
 某种项目的射击比赛,开始时在距目标100m处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已经在150m处,这时命中记2分,且停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200m处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分.已知射手甲在100m处击中目标的概率为
某种项目的射击比赛,开始时在距目标100m处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已经在150m处,这时命中记2分,且停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200m处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分.已知射手甲在100m处击中目标的概率为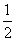 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
 (1)求这名射手分别在第二次、第三次射击中命中目标的概率及三次射击中命中目标的概率;
(1)求这名射手分别在第二次、第三次射击中命中目标的概率及三次射击中命中目标的概率;
 (2)设这名射手在比赛中得分数为
(2)设这名射手在比赛中得分数为 ,求随机变量
,求随机变量 的概率分布列和数学期望.
的概率分布列和数学期望.
16. (本小题满分12分)
(本小题满分12分)
 已知函数
已知函数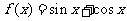 ,
,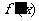 是
是 的导函数。
的导函数。
 (1)求函数
(1)求函数 的最大值和最小正周期;
的最大值和最小正周期;
 (2)若
(2)若 ,求
,求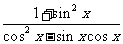 的值。
的值。
15. 设数列
设数列 的前
的前 项和为
项和为 ,令
,令 ,称
,称 为数列
为数列 ,
,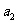 ,…,
,…, 的“理想数”,已知数列
的“理想数”,已知数列 ,
,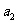 ,…,
,…,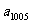 的“理想数”为
的“理想数”为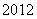 ,那么数列
,那么数列 ,
, ,
,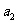 ,…,
,…,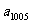 的“理想数”是
。
的“理想数”是
。
14. 双曲线的实轴长、虚轴长与焦距的和为8,则半焦距的取值范围是
。
双曲线的实轴长、虚轴长与焦距的和为8,则半焦距的取值范围是
。
13.由线性约束条件 所确定的区域面积为
所确定的区域面积为 ,当
,当 时,记
时,记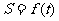 ,则
,则 的最大值为
。
的最大值为
。
12.已知 是单位向量,
是单位向量, ,则
,则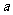 在
在 方向上的投影为
。
方向上的投影为
。
11. 若
若 的斜边
的斜边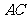 在平面
在平面 内,顶点
内,顶点 在平面
在平面 外,则两直角边
外,则两直角边 ,
, 在平面
在平面 上的射影与斜边
上的射影与斜边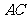 组成的图形是
。
组成的图形是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com