1．已知函数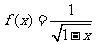在定义域为M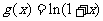，的定义域为N，则M∩N=(　　 )

　　　 A．{x|x＞1}　　　　　　 B．{x|x＜1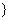　　　　　　 C．{x|-1＜x＜1　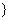　 D．

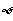
22．在平面直角坐标系中xOy中，过定点C(0，p)作直线与抛物线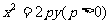相交

　　　 于A，B两点

　 (Ⅰ)若点N是点C关于坐标原点O的对称点，求△ANB面积的最小值；

　 (Ⅱ)是否存在垂直于y轴的直线l，使得l被以AC为直径的圆截得的弦长恒为定值？

　　　　 若存在，求出l的方程；若不存在，说明理由。(此题不要求在答题卡上画图)

21．若函数

　 (Ⅰ)求函数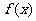的单调区间；

　 (Ⅱ)若方程(a为实数)在R上有三个不同实数根，求实数a的取值范围。

20．已知各项均为正数的等比数列{a_n}的首项为a₁=2，且4a₁是2a₂，a₃，的等差中项。

　 (Ⅰ)求数列{a_n}的通项公式a_n；

　 (Ⅱ)若，求。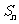

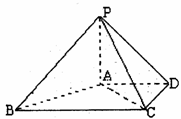
19．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，PA=AD=CD，BC=2AD，BC∥AD，

　　　 AD⊥DC。

　 (Ⅰ)证明AC⊥PB；

　 (Ⅱ)求二面角C-PB-A的大小。

18．网球单打冠军赛在甲、乙两人之间角逐，采用七局四胜制，即有一人先胜四场，则此人

　　　 获胜，且比赛结束。在每场比赛中，甲获胜的概率是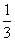，乙获胜的概率是。根据以往

　　　 资料统计，每场比赛组织者可获门票收入为30万元。两人决出胜负后，问：

　 (Ⅰ)求组织者在此决赛中获门票收入为120万元的概率？

　 (Ⅱ)求组织者在此决赛中获门票收入不低于180万元的概率？

17．设函数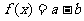，其中向量，且函数

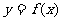　　　 的图象经过点

　 (Ⅰ)求实数m的值；

　 (Ⅱ)求函数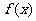的最小值及此时x的取值集合。

16．平面的斜线AB交于点B，过定点A的动直线l与AB垂直，且交于点C，则动

　　　 点C的轨迹是　　　　　　　 。

15．如果椭圆上存在一点P，使得点P到左准线的距离与它到右焦点

　　 的距离相等，那么椭圆的离心率的取值范围为　　　　　　　 。

14．若抛物线与直线相切，则此切线方程是　　　　　 。