5．沙河抽水蓄能电站自2003年投入运行以来，在缓解用电高峰电力紧张方面，取得了良好的社会效益和经济效益．抽水蓄能电站的工作原理是，在用电低谷时(如深夜)，电站利用电网多余电能把水抽到高处蓄水池中，到用电高峰时，再利用蓄水池中的水发电，如图18所示，蓄水池(上游水库)可视为长方体，有效总库容量(可用于发电)为V，蓄水后水位高出下游水面H，发电过程中上游水库水位最大落差为d.统计资料表明，该电站年抽水用电为2.4×10⁸ kW·h，年发电量为1.8×10⁸ kW·h.则下列计算结果正确的是(水的密度为ρ，重力加速度为g，涉及重力势能的计算均以下游水面为零势能面)(　)

A．能用于发电的水的最大重力势能E_p＝ρVgH

B．能用于发电的水的最大重力势能E_p＝ρVg

C．电站的总效率达75%

D．该电站平均每天所发电能可供给一个大城市居民用电(电功率以10⁵ kW计)约10 h

解析：以下游水面为零势能面，则用于发电的水的重心位置离下游水面高为(H－)，故其最大重力势能E_p＝ρVg(H－)，A错，B对；电站的总效率η＝×100%＝×100%＝75%，故C对；设该电站平均每天发电可供一个大城市居民用电t小时，则：Pt＝.代入数据得t＝5 h，故D错．

答案：BC

4．如图17所示，质量为M、长度为l的小车静止在光滑的水平面上．质量为m的小物块(可视为质点)放在小车的最左端．现用一水平恒力F作用在小物块上，使物块从静止开始做匀加速直线运动．物块和小车之间的摩擦力为f.物块滑到小车的最右端时，小车运动的距离为s.在这个过程中，以下结论正确的是(　)

A．物块到达小车最右端时具有的动能为(F－f)(l+s)

B．物块到达小车最右端时，小车具有的动能为fs

C．物块克服摩擦力所做的功为f(l+s)

D．物块和小车增加的机械能为Fs

解析：根据动能定理，物块到达最右端时具有的动能为E_k1＝ΔE_k1＝F·(l+s)－f·(l+s)＝(F－f)·(l+s)，A正确．物块到达最右端时，小车具有的动能可根据动能定理列式：E_k2＝ΔE_k2＝fs，B正确．由功的公式，物块克服摩擦力所做的功为W_f＝f(l+s)，C正确．物块增加的机械能E_km＝(F－f)(l+s)，小车增加的机械能E_kM＝fs，物块和小车增加的机械能为E_km+E_kM＝F·(l+s)－fl.或直接由功能关系得结论，D错误．

答案：ABC

图18

3．两个底面积都是S的圆筒，放在同一水平面上，桶内装水，水面高度分别为h₁和h₂，如图15所示．已知水的密度为ρ.现把连接两桶的阀门打开，最后两桶水面高度相等，则这过程中重力所做的功等于(　)

A.ρgS(h₁－h₂)²　 　　　　　　　　　　　　　　　 B．ρgS(h₁－h₂)²

C.ρgS(h₁－h₂)²　 　　　　　　　　　　　　　　　 D．ρgSh

图16

解析：由于水是不可压缩的，把连接两桶的阀门打开到两桶水面高度相等的过程中，利用等效法把左管高以上部分的水等效的移至右管．最后用功能关系，重力所做的功等于重力势能的减少量，阴影部分从左管移至右管所减少的重力势能为

ΔE_p＝()ρgS()＝ρgS(h₁－h₂)²

所以重力做的功W_G＝ρgS(h₁－h₂)²

答案：C

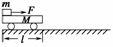
图17

2．如图14所示，一轻弹簧的左端固定，右端与一小球相连，小球处于光滑水平面上．现对小球施加一个方向水平向右的恒力F，使小球从静止开始运动，则小球在向右运动的整个过程中(　)

A．小球和弹簧组成的系统机械能守恒

B．小球和弹簧组成的系统机械能逐渐增大

C．小球的动能逐渐增大

D．小球的动能先增大然后减小

解析：小球在向右运动的整个过程中，力F做正功，由功能原理知小球和弹簧组成的系统机械能逐渐增大，选项A错误，选项B正确；弹力一直增大，当弹力等于F时，小球的速度最大，动能最大，当弹力大于F时，小球开始减速运动，速度减小，动能减小，选项C错误，选项D正确．

答案：BD

图15

1．在一种叫做“蹦极跳”的运动中，质量为m的游戏者身系一根长为L、弹性优良的轻质柔软橡皮绳，从高处由静止开始下落1.5L时到达最低点，若在下落过程中不计空气阻力，则从橡皮绳开始拉紧，到游戏者到达最低点的过程中，以下说法错误的是(　)

A．速度先增大后减小　　　　　　　　 B．加速度先减小后增大

C．动能增加了mgL　 　　　　　　　　　　　 D．重力势能减少了mgL

解析：橡皮绳拉紧的开始阶段：mg－F↑＝ma↓，a向下减小，但速度增加，当mg＝F以后，又有：F↑－mg＝ma′↑，a′向上增大，速度减小，故A、B正确；重力在此过程中做正功mgL，重力势能减少了mgL，D正确；因此过程初时刻动能为mgL，末时刻动能为0，动能减少了mgL，故C错误．

答案：C

图14

20、(本小题共12分)

已知.

(Ⅰ)求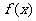的定义域；(Ⅱ)判断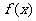的奇偶性；

(Ⅲ)求使的的取值范围。

抚顺县高中2010-2011学年度上学期高三年级第一次月考

19、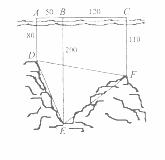 (本小题满分12分)

如图，为了解某海域海底构造，在海平面内一条直线上的A，B，C三点进行测量，已知，，于A处测得水深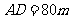，于B处测得水深，于C处测得水深，求∠DEF的余弦值。　　　　　　

18、(本小题共12分)

　　 在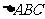中，角的对边分别为，.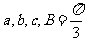

(Ⅰ)求的值；

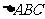(Ⅱ)求的面积.

17、(本小题共12分)

设函数的最小正周期为．

(Ⅰ)求的值．

(Ⅱ)若函数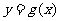的图像是由的图像向右平移个单位长度得到，求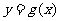 的单调增区间．

16、已知函数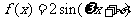的图像如图所示，则 　　　　　　　。