
4.已知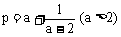 ,
,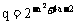 (a>2),则A
(a>2),则A
A、 p>q B、p<q C、p≥q D、p≤q
[填空题]
3.已知x>0,f(x)=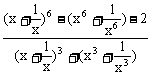 ,则
,则
A、f(x)≤2 B、f(x)≥10 C、f(x)≥6 D、f(x)≤3
2.若0<a<b且a+b=1,则四个数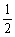 ,b,2ab,a2+b2中最大的是 ( )
,b,2ab,a2+b2中最大的是 ( )
A.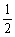 B、b
C、2ab
D、a2+b2
B、b
C、2ab
D、a2+b2
1.设x>0,y>0,且xy-(x+y)=1,则 ( )
A.x+y≤2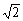 +2 B.x+y≥2
+2 B.x+y≥2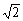 +2
+2
C.x+y≤(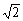 +1)2 D.x+y≥(
+1)2 D.x+y≥(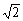 +1)2
+1)2
4.要熟练掌握均值不等式、四种平均值之间的关系,记住一些常用的不等式,记住它们的形式特点、证明方法和内在联系。
同步练习 6.3不等式的证明I
[选择题]
3.综合法是最简捷明快的方法,常需用分析法打前站,用分析法找路,综合法写出.有时也需要几种方法综合运用.
2.对较复杂的不等式需要用分析法,分析使不等式成立的充分条件,再证这个条件(不等式)成立.
1.比较法是一种最重要的、常用的基本方法,其应用非常广泛,一定要熟练掌握.
步骤是:作差→变形(分解因式或配方)→判断符号.
对于积或幂的式子可以作商比较,作商比较必须弄清两式的符号.
[例1](1)已知a,b∈R,求证: a2+b2+1>ab+a
(2)设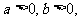 求证
求证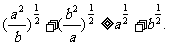
证明:(1)p= a2+b2+1-ab-a
=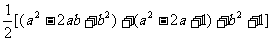
=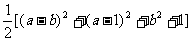
显然p>0 ∴得证
(2)证法一:左边-右边=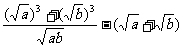
=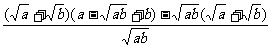
= 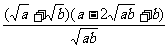 =
=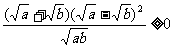 ∴原不等式成立。
∴原不等式成立。
证法二:左边>0,右边>0。
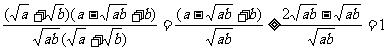 ∴原不等式成立。
∴原不等式成立。
◆提炼方法:比较法.作差(或商)、变形、判断三个步骤。变形的主要手段是通分、因式分解或配方。在变形过程中,也可以利用基本不等式放缩,如证法二。
[例2]已知a+b+c=0,求证:ab+bc+ca≤0.
证明法一:(综合法)∵a+b+c=0,
∴(a+b+c)2=0.
展开得ab+bc+ca=-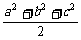 ,
,
∴ab+bc+ca≤0.
法二:(分析法)要证ab+bc+ca≤0,
∵a+b+c=0,
故只需证ab+bc+ca≤(a+b+c)2,
即证a2+b2+c2+ab+bc+ca≥0,
亦即证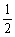 [(a+b)2+(b+c)2+(c+a)2]≥0.
[(a+b)2+(b+c)2+(c+a)2]≥0.
而这是显然的,由于以上相应各步均可逆,
∴原不等式成立.
证法三:∵a+b+c=0,∴-c=a+b.
∴ab+bc+ca=ab+(b+a)c=ab-(a+b)2
=-a2-b2-ab=-[(a+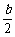 )2+
)2+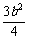 ]≤0.
]≤0.
∴ab+bc+ca≤0.
[例3]已知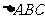 的三边长为
的三边长为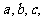 且
且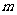 为正数.求证:
为正数.求证: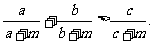
证明一:分析法: 要证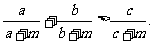
只需证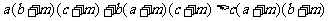
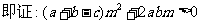 ①
①
∵在ΔABC中,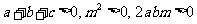
∴①式成立,从而原不等式成立.
证明二:比较法: 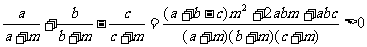

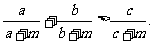
证明二: 因为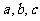 为
为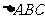 的三边长, 所以
的三边长, 所以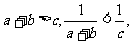
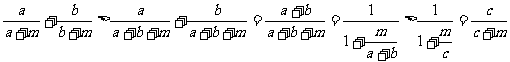
[例4]设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两根x1、x2满足1<x1<x2< .
.
(1)当x∈(0,x1)时,证明x<f(x)<x1;
(2)设函数f(x)的图象关于直线x=x0对称,求证x0<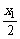 .
.
证明:(1)令F(x)=f(x)-x,
∵x1、x2是方程f(x)-x=0的根,
∴F(x)=a(x-x1)(x-x2).
当x∈(0,x1)时,由于x1<x2,
∴(x-x1)(x-x2)>0.
又a>0,得F(x)=a(x-x1)(x-x2)>0,
即x<f(x).
又x1-f(x)=x1-[x+F(x)]=x1-x+a(x1-x)(x-x2)=(x1-x)[1+a(x-x2)],
∵0<x<x1<x2< ,x1-x>0,
,x1-x>0,
1+a(x-x2)=1+ax-ax2>1-ax2>0,
∴x1-f(x)>0,即f(x)<x1.
综上,可知x<f(x)<x1.
(2)法1:f(x)=a(x-x1)(x-x2)+x=ax2-a(x1+x2-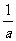 )x+ax1x2
)x+ax1x2
对称轴为x=x0=-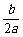 =
=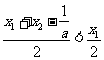 , (
, (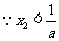 )
)
法2:由题意知x0=-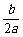 .
.
∵x1、x2是方程f(x)-x=0的根,
即x1、x2是方程ax2+(b-1)x+c=0的根,
∴x1+x2=-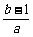 .
.
∴x0=-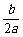 =
=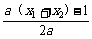 =
=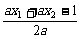 .
.
又∵ax2<1,∴x0<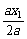 =
=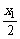 .
.
题目点评:函数或数列中的不等式,是高考中的一大类题目,应予以特别的关注,体会方法,积累经验.
[研讨.欣赏]已知a>1,m>0,求证:loga(a+m)>loga+m(a+2m).
证法1: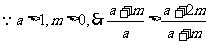
取对数得:lg(a+m)-lga>lg(a+2m)-lg(a+m)>0 ①
又 lga<log(a+m) 即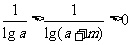 ②
②
①×②得: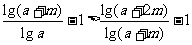
即loga(a+m)>loga+m(a+2m)
(常见形式logn(n+1)>log(n+1)(n+2))
法2:loga(a+m)-log(a+m)(a+2m)
=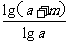 -
-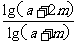
=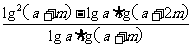
∵a>1,m>0,
∴lga>0,lg(a+2m)>0,且lga≠lg(a+2m).
∴lga·lg(a+2m)<[(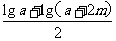 )]2
)]2
=[ ]2<[
]2<[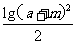 ]2=lg2(a+m).
]2=lg2(a+m).
∴ >0.
>0.
∴loga(a+m)>log(a+λ)(a+2m).
✿提炼方法:1.综合法,为什么想到用“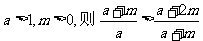 ”--感觉式子的结构特征;
”--感觉式子的结构特征;
2.比较法.把对数的积用均值 不等式化为对数的和是一步关键的决择.
6.设甲、乙距离为s,水流速度为v(v2>v>0),则船在流水中在甲乙间来回行驶一次的时间t=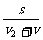 +
+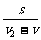 =
=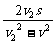 ,平均速度v1=
,平均速度v1=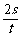 =
=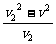 .
.
∵v1-v2=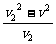 -v2=-
-v2=-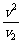 <0,
<0,
∴v1<v2.答案:v1<v2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com