
13.(1)谢公宿处今尚在, 。(李白《梦游天姥吟留别》)
(2) ,渺沧海之一粟。(苏轼《赤壁赋》)
(3)先帝不以臣卑鄙, , 。(诸葛亮《出师表》)
(4)江山代有才人出, ,(赵翼《论诗》)
(5) ,于我如浮云。(《论语》)
(6)穷则独善其身, 。(孟子·《尽心上》)
(7)青山遮不住, 。(辛弃疾《菩萨蛮·书江西造口壁》)
10. 求证:在非Rt△ABC中,若a>b,ha、hb分别表示a、b边上的高,则必有a+ha>b+hb.
证明:设S表示△ABC的面积,则
S=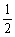 aha=
aha=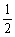 bhb=
bhb=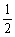 absinC.
absinC.
∴ha=bsinC,hb=asinC.
∴(a+ha)-(b+hb)=a+bsinC-b-asinC
=(a-b)(1-sinC).
∵C≠ ,∴1-sinC>0.
,∴1-sinC>0.
∴(a-b)(1-sinC)>0.
∴a+ha>b+hb.
[探索题]已知x,y,z∈(0,1)且x+y+z=2,记u=xy+yz+zx,求证: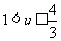
证明:3u=xy+yz+zx+2xy+2yz+2zx

= =4,故
=4,故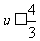 。又
。又
 三式相加得
三式相加得
 ,两边加上
,两边加上 得
得

∴ u>1,原不等式得证。
9. 设x>0,y>0且x≠y,求证
证明:由x>0,y>0且x≠y,要证明
只需 即
即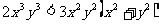
只需
由条件,显然成立.∴原不等式成立
8.己知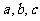 都是正数,且
都是正数,且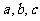 成等比数列,
成等比数列,
求证:
证明: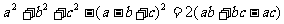

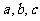 成等比数列,
成等比数列,

 都是正数,
都是正数,





7.(1)已知a、b、x、y∈R+且 >
>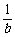 ,x>y. 求证:
,x>y. 求证: >
>
(2) 若a>0,b>0,a3+b3=2.求证a+b≤2,ab≤1.
证明(1)法一.(作差比较法)
∵ -
- =
= ,
,
又 >
>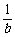 且a、b∈R+,
且a、b∈R+,
∴b>a>0.又x>y>0,∴bx>ay.
∴ >0,即
>0,即 >
> .
.
证法二:(分析法)
∵x、y、a、b∈R+,∴要证 >
> ,
,
只需证明x(y+b)>y(x+a),即证xb>ya.
而由 >
>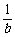 >0,∴b>a>0.又x>y>0,
>0,∴b>a>0.又x>y>0,
知xb>ya显然成立.故原不等式成立.
(2) (作差比较法)
因为a>0,b>0,a3+b3=2,所以
(a+b)3-23=a3+b3+3a2b+3ab2-8=3a2b+3ab2-6
=3[ab(a+b)-2]=3[ab(a+b)-(a3+b3)]=-3(a+b)(a-b)2≤0,
即 (a+b)3≤23.
又a+b>0,∴a+b≤2. 又∵ ∴ab≤1.
∴ab≤1.
6. 给出下列不等式,其中正确不等式的序号是_______
 ;
;
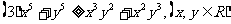 ,
,
◆练习简答:1-4. BBCA; 5.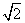 ; 6. (2)(3)
; 6. (2)(3)
[解答题]
5.要使不等式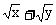 ≤
≤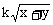 对所有正数x,y都成立,则k的最小值是_____
对所有正数x,y都成立,则k的最小值是_____
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com