
1.当且仅当事件 与事件
与事件 互相独立时,才有
互相独立时,才有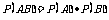 ,故首先要搞清两个事件的独立性.
,故首先要搞清两个事件的独立性.
4.n次独立重复试验中恰好发生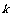 次的概率:如果在一次试验中某事件发生的概率是P,那么在
次的概率:如果在一次试验中某事件发生的概率是P,那么在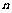 次独立重复试验中这个事件恰好发生
次独立重复试验中这个事件恰好发生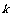 次的概率是
次的概率是 .
.
|
例1. 如图所示,用A、B、C三类不同的元件连接成两个系统 、
、 ,当元件A、B、C都正常工作时,系统
,当元件A、B、C都正常工作时,系统 正常工作,当元件A正常工作且元件B、C至少有1个正常工作时系统
正常工作,当元件A正常工作且元件B、C至少有1个正常工作时系统 正常工作,已知元件A、B、C正常工作的概率依次为0.8、0.9、0.9,分别求系统
正常工作,已知元件A、B、C正常工作的概率依次为0.8、0.9、0.9,分别求系统 、
、 正常工作时的概率.
正常工作时的概率.

解:分别记元件A、B、C正常工作为事件A、B、C,
由已知条件
(Ⅰ)因为事件A、B、C是相互独立的,所以,系统 正常工作的概率
正常工作的概率
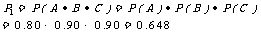 故系统
故系统 正常工作的概率为0.648.
正常工作的概率为0.648.
(Ⅱ)系统 正常工作的概率
正常工作的概率


故系统正常工作的概率为0.792.
变式训练1. 有甲、乙两地生产某种产品,甲地的合格率为90%,乙地的合格率为92%,从两地生产的产品中各抽取1 件,都抽到合格品的概率等于 ( )
A.112% B.9.2% C.82.8% D.0.8%
解:C
例2. 箱内有大小相同的20个红球,80个黑球,从中任意取出1个,记录它的颜色后再放回箱内,进行搅拌后再任意取出1个,记录它的颜色后又放回,假设三次都是这样抽取,试回答下列问题:
①求事件A:“第一次取出黑球,第二次取出红球,第三次取出黑球”的概率;
②求事件B:“三次中恰有一次取出红球”的概率.
解:(①  ;②
;② 
变式训练2:从甲袋中摸出一个红球的概率是 ,从乙袋中摸出1 个红球的概率是
,从乙袋中摸出1 个红球的概率是 ,从两袋中各摸出1个球,则
,从两袋中各摸出1个球,则 等于 ( )
等于 ( )
A.2个球不都是红球的概率
B.2个球都是红球的概率
C.至少有1个红球的概率
D.2个球中恰好有1个红球的概率
解:C
例3. 两台雷达独立工作,在一段时间内,甲雷达发现飞行目标的概率是0.9,乙雷达发现目标的概率是0.85,计算在这一段时间内,下列各事件的概率:
(1)甲、乙两雷达均未发现目标;
(2)至少有一台雷达发现目标;
(3)至多有一台雷达发现目标
解:①0.015; ②0.985; ③0.235
变式训练3:甲、乙、丙三人分别独立解一道题,甲做对的概率为 ,甲、乙、丙三人都做对的概率是
,甲、乙、丙三人都做对的概率是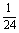 ,甲、乙、丙三人全做错的概率是
,甲、乙、丙三人全做错的概率是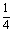 .
.
(1)求乙、丙两人各自做对这道题的概率;
(2)求甲、乙、丙三人中恰有一人做对这一道题的概率.
解: ① ,
, 或
或 ,
, ;②
;②
例4. 有三种产品,合格率分别为0.90,0.95和0.95,各取一件进行检验.
(1)求恰有一件不合格的概率;
(2)求至少有两件不合格的概率.(精确到0.01)
解:设三种产品各取一件,抽到的合格产品的事件分别为A、B和C
(Ⅰ)因为事件A、B、C相互独立,恰有一件不合格的概率为

答:恰有一件不合格的概率为0.176.
(Ⅱ)解法一:至少有两件不合格的概率为

答:至少有两件不合格的概率为0.012.
解法二:三件都合格的概率为:
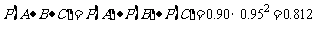
由(Ⅰ)可知恰好有一件不合格的概率为0.176,所以至少有两件不合格的概率为
 答:至少有两件不合格的概率为0.012.
答:至少有两件不合格的概率为0.012.
变式训练4. 甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为 .①分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;②从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
.①分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;②从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
|
 ,
, ,
, ;②
;②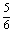
3.两个相互独立事件A,B同时发生的概率,等于每个事件发生的概率的积,即P(A·B)
=
一般地,如果事件 相互独立,那么:P(A1·A2……An)= .
相互独立,那么:P(A1·A2……An)= .
2.设A,B是两个事件,则A·B表示这样一个事件:它的发生,表示事件A,B ,类似地可以定义事件A1·A2·……An.
1.事件A(或B)是否发生对事件B(或A)发生的概率 ,这样的两个事件叫独立事件.
3.在求某些稍复杂的事件的概率时,通常有两种方法:一是将所求事件的概率化成一些彼此互斥事件的概率的和;二是先去求此事件的对立事件的概率.
第3课时 相互独立事件同时发生的概率
|
2.要搞清两个重要公式:
 的运用前提.
的运用前提.
1.互斥事件概率的加法公式、对立事件概率的加法公式,都必须在各个事件彼此互斥的前提下使用.
6.由于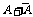 是一个必然事件,再加上
是一个必然事件,再加上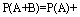
 ,故
,故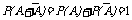 ,于是
,于是 ,这个公式很有用,常可使概率的计算得到简化.当直接求某一事件的概率较为复杂时,可转化去求其对立事件的概率.
,这个公式很有用,常可使概率的计算得到简化.当直接求某一事件的概率较为复杂时,可转化去求其对立事件的概率.
|
例1. 某射手在一次射击训练中,射中10环,9环,8环,7环的概率分别为0.21, 0.23, 0.25, 0.28,计算这个射手在一次射击中:①射中10环或7环的概率;②不够7环的概率.
解:① 0.49;② 0.03.
变式训练1. 一个口袋内有9张大小相同的票,其号数分别是1,2,3, ,9,从中任取2张,其号数至少有1个为偶数的概率等于 ( )
,9,从中任取2张,其号数至少有1个为偶数的概率等于 ( )
A. B.
B.
C. D.
D.
解:D
例2. 袋中有红、黄、白3种颜色的球各1只,从中每次任取1只,有放回地抽取3次,求:
(1)3只全是红球的概率.
(2)3只颜色全相同的概率.
(3)3只颜色不全相同的概率.
(4)3只颜色全不相同的概率.
解:(1)记“3只全是红球”为事件A.从袋中有放回地抽取3次,每次取1只,共会出现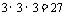 种等可能的结果,其中3只全是红球的结果只有一种,故事件A的概率为
种等可能的结果,其中3只全是红球的结果只有一种,故事件A的概率为 .
.
(2) “3只颜色全相同”只可能是这样三种情况:“3只全是红球”(事件A);“3只全是黄球”(设为事件B);“3只全是白球”(设为事件C).故“3只颜色全相同”这个事件为A+B+C,由于事件A、B、C不可能同时发生,因此它们是互斥事件.再由于红、黄、白球个数一样,故不难得 ,
,
故 .
.
(3) 3只颜色不全相同的情况较多,如是两只球同色而另一只球不同色,可以两只同红色或同黄色或同白色等等;或三只球颜色全不相同等.考虑起来比较麻烦,现在记“3只颜色不全相同”为事件D,则事件 为“3只颜色全相同”,显然事件D与
为“3只颜色全相同”,显然事件D与 是对立事件.
是对立事件.
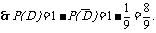
(4) 要使3只颜色全不相同,只可能是红、黄、白各一只,要分三次抽取,故3次抽到红、黄、白各一只的可能结果有 种,故3只颜色全不相同的概率为
种,故3只颜色全不相同的概率为
 .
.
变式训练2. 从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是 ( )
A.至少有1个黑球与都是黑球
B.至少有1个黑球与至少有1个红球
C.恰有1个黑球与恰有2个黑球
D.至少有1个黑球与都是红球
解:C
例3. 设人的某一特征(如眼睛大小)是由他的一对基因所决定的,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人是纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的一某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:①1个孩子有显性决定特征的概率是多少?②2个孩子至少有一个显性决定特征的概率是多少?
解:① ;②
;②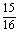
变式训练3. 盒中有6只灯泡,其中2只是次品,4只是正品,从其中任取两只,试求下列事件的概率:
① 取到两只都是次品;
② 取到两只中正品、次品各1只;
③ 取到两只中至少有1只正品.
解:⑴ ⑵
⑵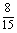 ⑶
⑶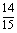
例4. 从男女学生共36名的班级中,任意选出2名委员,任何人都有同样的当选机会,如果选得同性委员的概率等于 ,求男女相差几名?
,求男女相差几名?
解: 设男生有 名,则女生有36-
名,则女生有36- 名,选得2名委员都是男生的概率为:
名,选得2名委员都是男生的概率为:
选得2名委员都是女生的概率为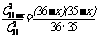
以上两种选法是互斥的,又选得同性委员的概率是
得: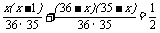
解得: 或
或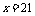
即:男生有15名,女生有21名;或男生有21名,女生有15名.总之,男、女生相差6名.
变式训练4. 学校某班学习小组共10小,有男生若干人,女生若干人,现要选出3人去参加某项调查活动,已知至少有一名女生去的概率为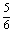 ,求该小组男生的人数?
,求该小组男生的人数?
解:6人
|
5.如果事件A、B互斥,那么事件A+B发生的概率,等于 .即P(A+B)= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com