
3.(2009全国卷II)下面文字中画线部分的词语,有的使用不当,请指出并改正,使这段文字语言简明,衔接自然,语意连贯。
苏泽广真是哭笑不得, 苏泽广①觉得儿子合图还不懂事,把家托付给他②是徒劳的,便失望地起身。然而他刚要离开,他③突然跳下椅子,合图④吹灭桌前的蜡烛,“扑通”一声跪在地上,抱住他⑤的腿,在黑暗中说:“爸爸,你放心吧,你⑥要是不回来,我⑦管这个家!
答:
。
[答案]①删除或改为“他”;③改为“合图”;④删除或改为“他”;⑤改为“苏泽广”或“父亲”。
[解析]①删除或改为“他”避免语意重复,达到简洁要求;③改为“合图”使指代明确;⑤改为“苏泽广”或“父亲” 使指代明确;使前后文衔接、连贯。
[考点定位]本题重点考查考生语言表达简明、衔接、连贯的能力,同时与病句修改结合起来。因此,要在语句通畅的基础上,力求连贯得体。
2.(2009全国卷I)下面是“沈阳全民读书月”活动的标识,请从构形角度说明标识的创意,要求语意简明,句子通顺,不超过65个字。

答:
。
[答案]示例:该标识以“书”和“沈阳”的首写拼音字母为设计元素,体现活动的主题与地狱;翻开的书和两书交汇处的眼睛,对“开卷有益”作出微妙表达。
[解析]解答时要扣住主题“沈阳全民读书月”,要特别突出“沈阳”和“读书”两个词语的图形构成,同时结合题干要求“从构形角度说明标识的创意”,进行整合,语言要求流畅、富有文采。注意字数要求。
[考点定位]本体为图文转换试题,既考查考生语言表达简明、连贯、得体的能力。
1.(2009全国卷I)下面文字中画线的部分的词语,有的使用不当,请指出并改正,使修改后的这段文字衔接自然,语意连贯,逻辑严密。
三仙姑对女儿小芹一直管得很严。小芹①后,跟小二黑②好上了,三仙姑说什么也不同意。她③道后,就一个人悄悄跑到前庄上去找小二黑④恰巧小二黑这时也正要找她,于是两个人就商量对付她⑤的办法。她⑥把小芹娘⑦的事从关至尾向小二黑细说了一遍。
答:
。
[答案]③改为“小芹”;⑤改为“三仙姑”⑥ 改为“小芹”;⑦ 改为“她”。
[解析]本题重点考查考生语言表达衔接、连贯的能力,③⑤⑥用“她”指代不明,⑦用“小芹”则会造成叠床架屋,语意重复。
[考点定位]本题重点考查病句修改能力及语言表达衔接、连贯的能力。
18.(2010湖南文数)(本小题满分12分)
 如图所示,在长方体
如图所示,在长方体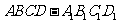 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点
(Ⅰ)求异面直线A1M和C1D1所成的角的正切值;
(Ⅱ)证明:平面ABM⊥平面A1B1M1

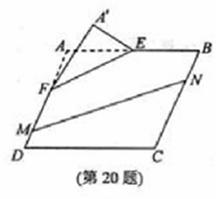 (2010浙江理数)(20)(本题满分15分)如图, 在矩形
(2010浙江理数)(20)(本题满分15分)如图, 在矩形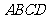 中,点
中,点 分别在线段
分别在线段 上,
上, .沿直线
.沿直线 将
将 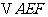 翻折成
翻折成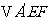 ,使平面
,使平面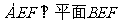 .
.
(Ⅰ)求二面角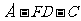 的余弦值;
的余弦值;
(Ⅱ)点 分别在线段
分别在线段 上,若沿直线
上,若沿直线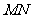 将四边形
将四边形 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段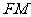 的长。
的长。
解析:本题主要考察空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同事考查空间想象能力和运算求解能力。
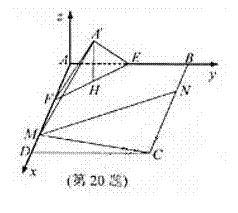 (Ⅰ)解:取线段EF的中点H,连结
(Ⅰ)解:取线段EF的中点H,连结 ,因为
,因为 =
= 及H是EF的中点,所以
及H是EF的中点,所以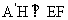 ,
,
又因为平面 平面
平面 .
.
如图建立空间直角坐标系A-xyz
则 (2,2,
(2,2, ),C(10,8,0),
),C(10,8,0),
F(4,0,0),D(10,0,0).
故 =(-2,2,2
=(-2,2,2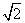 ),
), =(6,0,0).
=(6,0,0).
设 =(x,y,z)为平面
=(x,y,z)为平面 的一个法向量,
的一个法向量,
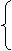 -2x+2y+2
-2x+2y+2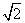 z=0
z=0
所以
6x=0.
取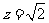 ,则
,则 。
。
又平面 的一个法向量
的一个法向量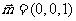 ,
,
故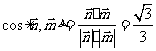 。
。
所以二面角的余弦值为
(Ⅱ)解:设 则
则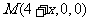 ,
,
因为翻折后, 与
与 重合,所以
重合,所以 ,
,
故,  ,得
,得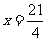 ,
,
经检验,此时点 在线段
在线段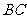 上,
上,
所以 。
。
 方法二:
方法二:
(Ⅰ)解:取线段 的中点
的中点 ,
, 的中点
的中点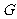 ,连结
,连结 。
。
因为 =
=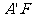 及
及 是
是 的中点,
的中点,
所以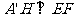
又因为平面
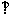 平面
平面 ,
,
所以 平面
平面 ,
,
又 平面
平面 ,
,
故
 ,
,
又因为 、
、 是
是 、
、 的中点,
的中点,
易知 ∥
∥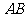 ,
,
所以
 ,
,
于是
 面
面 ,
,
所以 为二面角
为二面角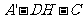 的平面角,
的平面角,
在 中,
中,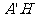 =
= ,
, =2,
=2, =
=
所以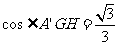 .
.
故二面角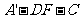 的余弦值为
的余弦值为 。
。
(Ⅱ)解:设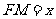 ,
,
因为翻折后, 与
与 重合,
重合,
所以 ,
,
而 ,
,

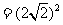
得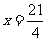 ,
,
经检验,此时点 在线段
在线段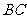 上,
上,
所以 。
。
(2010全国卷2理数)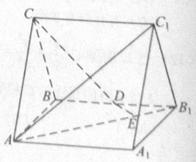 (19)如图,直三棱柱
(19)如图,直三棱柱 中,
中,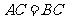 ,
, ,
,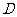 为
为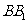 的中点,
的中点,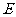 为
为 上的一点,
上的一点, .
.
(Ⅰ)证明: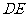 为异面直线
为异面直线 与
与 的公垂线;
的公垂线;
 (Ⅱ)设异面直线
(Ⅱ)设异面直线 与
与 的夹角为45°,求二面角
的夹角为45°,求二面角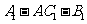 的大小.
的大小.
[命题意图]本试题主要考查空间的线面关系与空间角的求解,考查考生的空间想象与推理计算的能力.
20.(2010上海文数)(本大题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
 如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用 平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
(1)当圆柱底面半径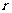 取何值时,
取何值时, 取得最大值?并求出该
取得最大值?并求出该
最大值(结果精确到0.01平方米);
(2)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出
用于灯笼的三视图(作图时,不需考虑骨架等因素).
解析:(1) 设圆柱形灯笼的母线长为l,则l=1.2-2r(0<r<0.6),S=-3p(r-0.4)2+0.48p, 所以当r=0.4时,S取得最大值约为1.51平方米; (2) 当r=0.3时,l=0.6,作三视图略.
21.(2010江苏卷)[选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答。若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。
E.  选修4-1:几何证明选讲
选修4-1:几何证明选讲
(本小题满分10分)
AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DA=DC,求证:AB=2BC。
[解析] 本题主要考查三角形、圆的有关知识,考查推理论证能力。
 (方法一)证明:连结OD,则:OD⊥DC,
(方法一)证明:连结OD,则:OD⊥DC,
又OA=OD,DA=DC,所以∠DAO=∠ODA=∠DCO,
∠DOC=∠DAO+∠ODA=2∠DCO,
所以∠DCO=300,∠DOC=600,
所以OC=2OD,即OB=BC=OD=OA,所以AB=2BC。
(方法二)证明:连结OD、BD。
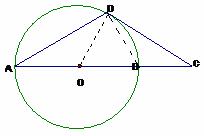 因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为DC 是圆O的切线,所以∠CDO=900。
又因为DA=DC,所以∠DAC=∠DCA,
于是△ADB≌△CDO,从而AB=CO。
即2OB=OB+BC,得OB=BC。
故 AB=2BC。
AB=2BC。
F. 选修4-2:矩阵与变换
(本小题满分10分)
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M= ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
[解析] 本题主要考查图形在矩阵对应的变换下的变化特点,考查运算求解能力。满分10分。
解:由题设得
由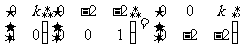 ,可知A1(0,0)、B1(0,-2)、C1(
,可知A1(0,0)、B1(0,-2)、C1(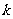 ,-2)。
,-2)。
计算得△ABC面积的面积是1,△A1B1C1的面积是 ,则由题设知:
,则由题设知: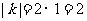
 。
。
所以k的值为2或-2。
G.选修4-4:坐标系与参数方程
(本小题满分10分)
在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值。
[解析] 本题主要考查曲线的极坐标方程等基本知识,考查转化问题的能力。满分10分。
解: ,圆ρ=2cosθ的普通方程为:
,圆ρ=2cosθ的普通方程为: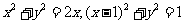 ,
,
直线3ρcos θ+4ρsinθ+a=0的普通方程为:
θ+4ρsinθ+a=0的普通方程为: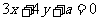 ,
,
又圆与直线相切,所以 解得:
解得: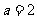 ,或
,或 。
。
H. 选修4-5:不等式选讲
(本小题满分10分)
设a、b是非负实数,求证: 。
。
[解析] 本题主要考查证明不等式的基本方法,考查推理论证的能力。满分10分。
(方法一)证明: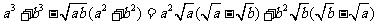
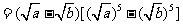

因为实数a、b≥0,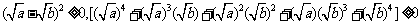
所以上式 ≥0。即有
≥0。即有 。
。
(方法二)证明:由a、b是非负实数,作差得
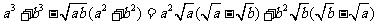
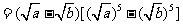
当 时,
时, ,从而
,从而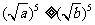 ,得
,得 ;
;
当 时,
时, ,从而
,从而 ,得
,得 ;
;
所以 。
。
[必做题]第22题、第23题,每题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
21.(2010江苏卷)[选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答。若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。
A.  选修4-1:几何证明选讲
选修4-1:几何证明选讲
(本小题满分10分)
AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DA=DC,求证:AB=2BC。
[解析] 本题主要考查三角形、圆的有关知识,考查推理论证能力。
 (方法一)证明:连结OD,则:OD⊥DC,
(方法一)证明:连结OD,则:OD⊥DC,
又OA=OD,DA=DC,所以∠DAO=∠ODA=∠DCO,
∠DOC=∠DAO+∠ODA=2∠DCO,
所以∠DCO=300,∠DOC=600,
所以OC=2OD,即OB=BC=OD=OA,所以AB=2BC。
(方法二)证明:连结OD、BD。
 因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为DC 是圆O的切线,所以∠CDO=900。
又因为DA=DC,所以∠DAC=∠DCA,
于是△ADB≌△CDO,从而AB=CO。
即2OB=OB+BC,得OB=BC。
故 AB=2BC。
AB=2BC。
B. 选修4-2:矩阵与变换
(本小题满分10分)
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M= ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
[解析] 本题主要考查图形在矩阵对应的变换下的变化特点,考查运算求解能力。满分10分。
解:由题设得
由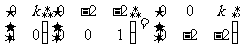 ,可知A1(0,0)、B1(0,-2)、C1(
,可知A1(0,0)、B1(0,-2)、C1(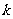 ,-2)。
,-2)。
计算得△ABC面积的面积是1,△A1B1C1的面积是 ,则由题设知:
,则由题设知: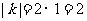
 。
。
所以k的值为2或-2。
C. 选修4-4:坐标系与参数方程
(本小题满分10分)
在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值。
[解析] 本题主要考查曲线的极坐标方程等基本知识,考查转化问题的能力。满分10分。
解: ,圆ρ=2cosθ的普通方程为:
,圆ρ=2cosθ的普通方程为: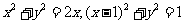 ,
,
直线3ρcos θ+4ρsinθ+a=0的普通方程为:
θ+4ρsinθ+a=0的普通方程为: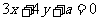 ,
,
又圆与直线相切,所以 解得:
解得: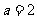 ,或
,或 。
。
D.选修4-5:不等式选讲
(本小题满分10分)
设a、b是非负实数,求证: 。
。
[解析] 本题主要考查证明不等式的基本方法,考查推理论证的能力。满分10分。
(方法一)证明: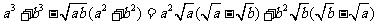
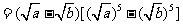

因为实数a、b≥0,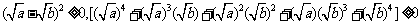
所以上式 ≥0。即有
≥0。即有 。
。
(方法二)证明:由a、b是非负实数,作差得
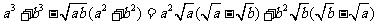
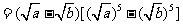
当 时,
时, ,从而
,从而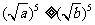 ,得
,得 ;
;
当 时,
时, ,从而
,从而 ,得
,得 ;
;
所以 。
。
[必做题]第22题、第23题,每题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
2010年高考数学试题分类汇编--新课标选考内容
(2010辽宁理数)(22)(本小题满分10分)选修4-1 :几何证明选讲
:几何证明选讲
 如图,
如图, 的角平分线AD的延长线交它的外接圆于点E
的角平分线AD的延长线交它的外接圆于点E
(I)证明:

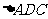
(II)若 的面积
的面积 ,求
,求 的大小。
的大小。
证明:
(Ⅰ)由已知条件,可得
因为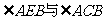 是同弧上的圆周角,所以
是同弧上的圆周角,所以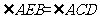
故△ABE∽△ADC.
…
 …5分
…5分
(Ⅱ)因为△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S= AB·ACsin
AB·ACsin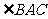 ,且S=
,且S= AD·AE,故AB·ACsin
AD·AE,故AB·ACsin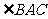 =
AD·AE.
=
AD·AE.
则sin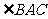 =1,又
=1,又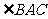 为三角形内角,所以
为三角形内角,所以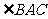 =90°.
……10分
=90°.
……10分
(2010辽宁理数)(23)(本小题满分10分)选修4-4:坐标系与参数方程
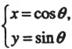
已知 P为半圆C:
(
P为半圆C:
( 为参数,
为参数, )上的点,点A的坐标为(1,0),
)上的点,点A的坐标为(1,0),
O为坐标原点,点M在射线OP上,线段OM与C的弧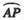 的长度均为
的长度均为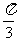 。
。
(I)以O为极点,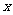 轴的正半轴为极轴建立极坐标系,求点M的极坐标;
轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(II)求直线AM的参数方程。
解:
(Ⅰ)由已知,M点的极角为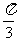 ,且M点的极径等于
,且M点的极径等于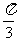 ,
,
故点M的极坐标为(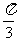 ,
,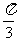 ).
……5分
).
……5分
(Ⅱ)M点的直角坐标为(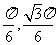 ),A(0,1),故直线AM的参数方程为
),A(0,1),故直线AM的参数方程为
 (t为参数)
……10分
(t为参数)
……10分
(2010辽宁理数)(24)(本小题满分10分)选修4-5:不等式选讲
已知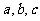 均为正数,证明:
均为正数,证明: ,并确定
,并确定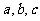
 为何值时,等号成立。
为何值时,等号成立。
证明:(证法一)
因为a,b,c均为正数,由平均值不等式得
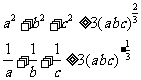 ①
①
所以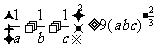 ②
……6分
②
……6分
故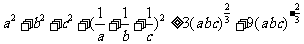 .
.
又 ③
③
所以原不等式成立.
 ……8分
……8分
当且仅当a=b=c时,①式和②式等号成立。当且仅当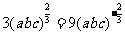 时,③式等号成立。
时,③式等号成立。
即当且仅当a=b=c= 时,原式等号成立。
……10分
时,原式等号成立。
……10分
(证法二)
因为a,b,c均为正数,由基本不等式得

所以 ①
①
同理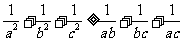 ②
……6分
②
……6分
故
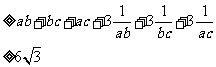 ③
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c, 时,③式等号成立。
时,③式等号成立。
即当且仅当a=b=c= 时,原式等号成立。
……10分
时,原式等号成立。
……10分
21.(2010福建理数)本题设有(1)(2)(3)三个选考题,每题7分,请考生任选2题做答,满分14分。如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵M=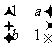 ,
,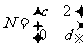 ,且
,且 ,
,
(Ⅰ)求实数 的值;(Ⅱ)求直线
的值;(Ⅱ)求直线 在矩阵M所对应的线性变换下的像的方程。
在矩阵M所对应的线性变换下的像的方程。
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标系xoy中,直线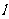 的参数方程为
的参数方程为 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 。
。
(Ⅰ)求圆C的直角坐标方程;(Ⅱ)设圆C与直线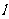 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为 ,
,
求|PA|+|PB|。
(3)(本小题满分7分)选修4-5:不等式选讲
已知函数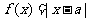 。K^S*5U.C#O%
。K^S*5U.C#O%
(Ⅰ)若 不等式
不等式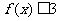 的解集为
的解集为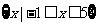 ,求实数
,求实数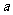 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若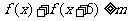 对一切实数x恒成立,求实数m的取值范围。
对一切实数x恒成立,求实数m的取值范围。
(1)选修4-2:矩阵与变换
[命题意图]本小题主要考查矩 阵与变换等基础知识,考查运算求解能力。K^S*5U.C#O%
阵与变换等基础知识,考查运算求解能力。K^S*5U.C#O%
[解析](Ⅰ)由题设得 ,解得
,解得 ;
;
(Ⅱ)因为矩阵M所对应的线性变换将直线变成直线(或点),所以可取直线 上的两(0,0),(1,3),
上的两(0,0),(1,3),
由
 ,
,
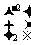 得:点(0,0),(1,3)在矩阵M所对应的线性变换下的像是(0,0),(-2,2),从而直线
得:点(0,0),(1,3)在矩阵M所对应的线性变换下的像是(0,0),(-2,2),从而直线 在矩阵M所对应的线性变换下的像的方程为
在矩阵M所对应的线性变换下的像的方程为 。
。
(2)选修4-4:坐标系与参数方程
[命题意图]本小题主要考查直线的参数方程、圆的极坐标方程、直线与圆的位置关系等基础知识,考查运算求解能力。
[解析](Ⅰ)由 得
得 即
即
 (Ⅱ)将
(Ⅱ)将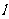 的参数方程代入圆C的直角坐标方程,得
的参数方程代入圆C的直角坐标方程,得 ,
,
即 由于
由于 ,故可设
,故可设 是上述方程的两实根,
是上述方程的两实根,
所以 故由上式及t的几何意义得:
故由上式及t的几何意义得:
|PA|+|PB|=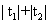 =
=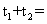
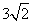 。
。
(3)选修4-5:不等式选讲
[命题意图]本小题主要考查绝对值的意义、绝对值不等式等基础知识,考查运 算求解能力。
算求解能力。
[解析](Ⅰ)由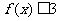 得
得 ,解得
,解得 ,
,
又已知不等式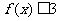 的解集为
的解集为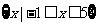 ,所以
,所以 ,解得
,解得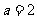 。
。
(Ⅱ)当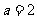 时,
时, ,设
,设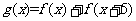 ,于是
,于是
 =
= ,所以
,所以
当 时,
时,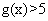 ;当
;当 时,
时,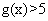 ;当
;当 时,
时,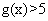 。
。
20.(2010湖南文数)(本小题满分13分)
给出下面的数表序列:

其中表n(n=1,2,3  )有n行,第1行的n个数是1,3,5,
)有n行,第1行的n个数是1,3,5, 2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和。
2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和。
(I)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明);
(II)每个数列中最后一行都只有一个数,它们构成数列1,4,12 ,记此数列为
,记此数列为
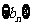 求和:
求和:




(2010全国卷2理数)(18)(本小题满分12分)
已知数列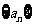 的前
的前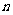 项和
项和 .
.
(Ⅰ)求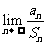 ;
;
(Ⅱ)证明: .
.
[命题意图]本试题主要考查数列基本公式 的运用,数列极限和数列不等式的证明,考查考生运用所学知识
的运用,数列极限和数列不等式的证明,考查考生运用所学知识 解决问题的能力.
解决问题的能力.
21.(2010上海文数)(本题满分14分)本题共有2个小题,第一个小题满分6分,第2个小题满分8分。
已知数列 的前
的前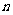 项和为
项和为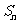 ,且
,且 ,
,
(1)证明: 是等比数列;
是等比数列;
(2)求数列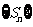 的通项公式,并求出使得
的通项公式,并求出使得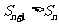 成立的最小正整数
成立的最小正整数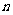 .
.
解析:(1) 当n=1时,a1=-14;当n≥2时,an=Sn-Sn-1=-5an+5an-1+1,所以 ,
又a1-1=-15≠0,所以数列{an-1}是等比数列;
(2) 由(1)知:
,
又a1-1=-15≠0,所以数列{an-1}是等比数列;
(2) 由(1)知: ,得
,得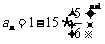 ,从而
,从而 (nÎN*);
由Sn+1>Sn,得
(nÎN*);
由Sn+1>Sn,得 ,
, ,最小正整数n=15.
,最小正整数n=15.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com