
2、不等式组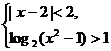 的解集为 ( )
的解集为 ( )
A.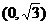 B
B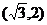 C.
C.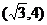 D.
D.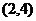
1、复数-i的一个立方根是i,它的另外两个立方根是…………………………( )
A)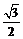 ±
±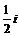 B)-
B)-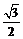 ±
±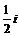 C)±
C)±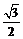 +
+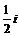 D)±
D)±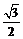 -
-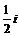
10. 已知a、b为正数,求证:
(1)若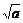 +1>
+1>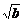 ,则对于任何大于1的正数x,恒有ax+
,则对于任何大于1的正数x,恒有ax+ >b成立;
>b成立;
(2)若对于任何大于1的正数x,恒有ax+ >b成立,则
>b成立,则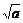 +1>
+1>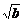 .
.
分析:对带条件的不等式的证明,条件的利用常有两种方法:①证明过程中代入条件;②由条件变形得出要证的不等式.
证明:(1)ax+ =a(x-1)+
=a(x-1)+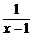 +1+a≥2
+1+a≥2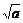 +1+a=(
+1+a=(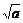 +1)2.
+1)2.
∵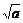 +1>
+1>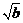 (b>0),
(b>0),
∴(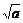 +1)2>b.从而ax+
+1)2>b.从而ax+ >b
>b
(2)∵ax+ >b对于大于1的实数x恒成立,即x>1时,[ax+
>b对于大于1的实数x恒成立,即x>1时,[ax+ ]min>b,
]min>b,
而ax+ =a(x-1)+
=a(x-1)+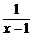 +1+a≥2
+1+a≥2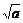 +1+a=(
+1+a=(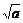 +1)2,
+1)2,
当且仅当a(x-1)=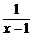 ,即x=1+
,即x=1+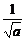 >1时取等号.
>1时取等号.
故[ax+ ]min=(
]min=(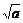 +1)2.
+1)2.
则(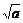 +1)2>b,即
+1)2>b,即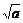 +1>
+1>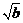 .
.
评述:条件如何利用取决于要证明的不等式两端的差异如何消除.
[探索题](2005湖北)已知不等式 , 其中n为大于2的整数,
, 其中n为大于2的整数,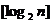 表示不超过
表示不超过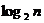 的最大整数. 设数列
的最大整数. 设数列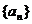 的各项为正,且满足
的各项为正,且满足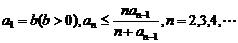
(Ⅰ)证明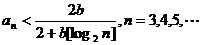
(Ⅱ)试确定一个正整数N,使得当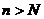 时,对任意b>0,都有
时,对任意b>0,都有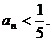
解:(Ⅰ)证法1:∵当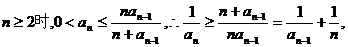
即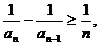
于是有 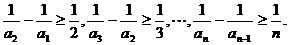
所有不等式两边相加可得 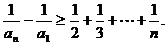
由已知不等式知,当n≥3时有,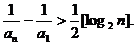
∵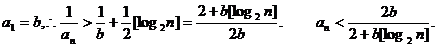
证法2:设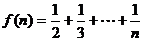 ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式
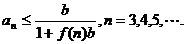
(i)当n=3时, 由 
知不等式成立.
(ii)假设当n=k(k≥3)时,不等式成立,即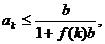
则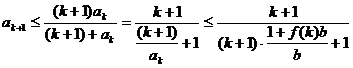
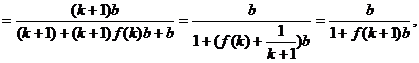
即当n=k+1时,不等式也成立.
由(i)、(ii)知,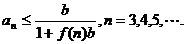
又由已知不等式得 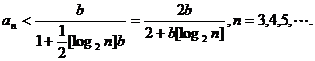
(Ⅱ)∵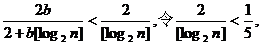
则有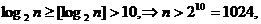
故取N=1024,可使当n>N时,都有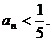
9.若a>0, b>0,且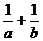 =1,
=1,
求证:(I) a+b≥4;
(II) 对于一切n∈N*, (a+b)n-an-bn≥22n-2n+1成立
证明:(I) 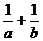 =1, a+b=(
=1, a+b=(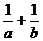 )(a+b)=1+
)(a+b)=1+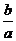 +
+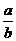 +1≥4,
+1≥4,
(II) 当n=1时, 左式=0,右式=0,∴n=1时成立.
假设n=k时成立,即(a+b)k-ak-bk≥22k-2k+1,.
则当n=k+1时,(a+b)k+1-ak+1-bk+1
=(a+b) (a+b)k-ak+1-bk+1
≥(a+b)(ak+bk+22k-2k+1) -ak+1-bk+1
=abk+bak+(a+b)(22k-2k+1)
≥2·2k+1+4·22k-4·2k+1=22k+2-2k+2,
∴n=k+1时命题成立.归纳原理知,不等式对一切n∈N*都成立
8. 设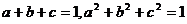 ,且
,且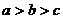 ,求证:
,求证: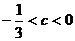
因为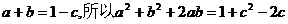 ,而
,而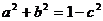
所以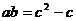 ,所以a,b为方程
,所以a,b为方程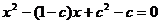 (1)的二实根
(1)的二实根
而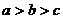 ,故方程(1)有均大于c的二不等实根。
,故方程(1)有均大于c的二不等实根。
记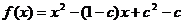 ,则
,则
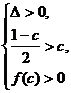 解得
解得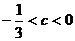 。
。
法2: 由已知得c<0, 否则,由(a+b+c)2=1得
A2+b2+c2=1-2(ab+bc+ac)<1,与已知矛盾.
又a+b=1-c代入c2=1-(a2+b2)得3c2-2c-1<0,
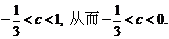
7.已知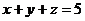 ,
,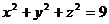 求证:
求证: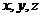 都属于
都属于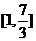 。
。
[证明]由已知得: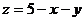 ,代入
,代入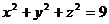 中得:
中得:
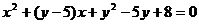
∵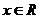 ,∴△≥0,即
,∴△≥0,即
解得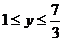 ,即y∈
,即y∈ 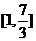 。同理可证x∈
。同理可证x∈ 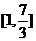 ,z∈
,z∈ 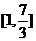 。
。
6. 记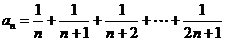 ,则
,则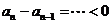 ,
,
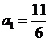 最大. M>1
最大. M>1
[解答题]
6.已知不等式 对n∈N+都成立,则实数M的取值范围是__________。
对n∈N+都成立,则实数M的取值范围是__________。
简答.提示:1-4.ADAB; 5. ax+ay≥2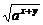 =2
=2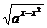 .
.
∵x-x2=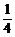 -(x-
-(x-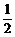 )2≤
)2≤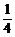 ,0<a<1,∴ax+ay≥2
,0<a<1,∴ax+ay≥2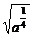 =2a
=2a .
.
∴loga(ax+ay)<loga2a =loga2+
=loga2+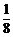 .即P<Q;
.即P<Q;
5. 设实数x、y满足y+x2=0,0<a<1.则P=loga(ax+ay)与Q=loga2+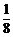 的大小关系是___________(填“>”“=”“<”).
的大小关系是___________(填“>”“=”“<”).
4. (2005江西)已知实数a、b满足等式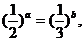 下列五个关系式:
下列五个关系式:
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有 ( )
A.1个 B.2个 C.3个 D.4个
[填空题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com