13．(2009·天津高考)如图是一个几何体的三视图．若它的体积是3，则a＝________.

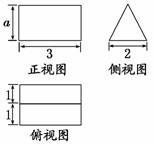
解析：由三视图知该几何体的直观图为直三棱柱(如图)．

其中△ABC是以BC＝2为底的等腰三角形，CC₁＝3.

∴V＝S_△ABC×3＝×2×a×3＝3.故a＝.

答案：

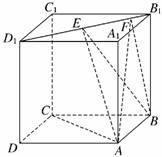
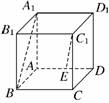
12．(2009·宁夏、海南高考)如图，正方体ABCD－A₁B₁C₁D₁

的棱长为1，线段B₁D₁上有两个动点E、F，且EF＝，则

下列结论中错误的是　　　　　　　　　　　　　 (　)

A．AC⊥BE

B．EF∥平面ABCD

C．三棱锥A－BEF的体积为定值

D．△AEF的面积与△BEF的面积相等

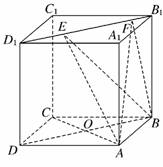解析：如图，正方体ABCD－A₁B₁C₁D₁中，

AC⊥BD，AC⊥BB₁，

BD∩BB₁＝B，∴AC⊥平面BB₁D₁D，

BE⊂平面BB₁D₁D，

∴AC⊥BE，∴A对．

∵EF∥DB，∴EF∥平面ABCD，∴B对．

S_△BEF＝×EF×BB₁＝××1＝，

AO⊥平面BB₁D₁D，AO＝，

∴V_A－BEF＝××＝，

∴三棱锥的体积为定值，C对．

答案：D

11．已知三个平面α、β、γ，若β⊥γ，且α与β、α与γ均相交但不垂直，a、b分别为α、β内的直线，则　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．∀b⊂β，b⊥γ　 　　　　　　　B．∀b⊂β，b∥γ

C．∃a⊂α，a⊥γ 　　　　　　　　D．∃a⊂α，a∥γ

解析：选项A中β⊥γ，但并不是平面β内的任意直线都与平面γ垂直，故选项A不正确；由于β⊥γ，只有在平面β内与平面β与γ的交线平行的直线才和平面γ平行，选项B不正确；若存在a⊂α，a⊥γ，则必然α⊥γ，选项C不正确；只要在平面α内存在与平面α与γ的交线平行的直线，则此直线平行于平面γ，故选项D正确．

答案：D

10．(文)如图，已知△ABC为直角三角形，其中∠ACB＝90°，M为AB中点，PM垂直于△ABC所在平面，那么 　　　　　　　　　　　　　　　　　　　　　　　(　)

A．PA＝PB＞PC

B．PA＝PB＜PC

C．PA＝PB＝PC

D．PA≠PB≠PC

解析：∵M是Rt△ABC斜边AB的中点，

∴MA＝MB＝MC.

又∵PM⊥平面ABC，∴MA、MB、MC分别是PA、PB、PC在平面ABC上的射影．∴PA＝PB＝PC.应选C.

答案：C

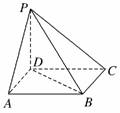
(理)如右图所示，点P在正方形ABCD所在平面外，

PD⊥平面ABCD，PD＝AD，则PA与BD所成角的

度数为　　　　　 　　　　　　　　　　　　　(　)

A．30°　　　　 　B．45°　　　　　 C．60° 　　　　　D．90°

解析：以DA、DC、DP为邻边构造正方体BP，易知PA与BD所成的角为60°.

答案：C

9．已知两条不同直线l₁和l₂及平面α，则直线l₁∥l₂的一个充分条件是　　　　 (　)

A．l₁∥α且l₂∥α　　　　　　　　 　B．l₁⊥α且l₂⊥α

C．l₁∥α且l₂⊄α　 　　　　　　　　　D．l₁∥α且l₂⊂α

解析：对选项A，l₁与l₂还可能相交或成异面直线，A错．根据直线与平面垂直的性质定理，B正确．另外，对于选项C，l₁与l₂不一定平行，C错．对于选项D，l₁与l₂还可能为异面直线．

答案：B

8．一个几何体的三视图如图所示，其中正视图和侧视

图是腰长为1的两个全等的等腰直角三角形，则该

几何体的外接球的表面积为　　　　　　 　　(　)

A．12π　　　　　　　　　　　 　B．4π

C．3π　　　　　　　　　　　 　D．12π

解析：由三视图知该几何体为四棱锥，记作S－ABCD，

其中SA⊥面ABCD.面ABCD为正方形，将此四棱锥还原为正方体，易知正方体的体对角线即为外接球直径，所以2r＝.∴S_球＝4πr²＝4π×＝3π.

答案：C

7．(2009·广东高考)给定下列四个命题：

①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；

②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；

③垂直于同一直线的两条直线相互平行；

④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．

其中，为真命题的是　　 　　　　　　　　　　　　　　　　　　　　　　　(　)

A．①和②　　　　　　　　　 　B．②和③

C．③和④　 　　　　　　　　　D．②和④

解析：①显然错误，因为这两条直线相交时才满足条件；②成立；③错误，这两条直线可能平行，相交，也可能异面；④成立，用反证法容易证明．

答案：D

6．如图，在正方体ABCD－A₁B₁C₁D₁中，若E是AD的中点，

则直线A₁B与直线C₁E的位置关系是　　　　　　 (　)

A．平行　　　　　　 　　B．相交

C．共面　　　　　　 　　D．垂直

解析：易证A₁B⊥平面AB₁C₁D，又C₁E⊂平面AB₁C₁D，

∴A₁B⊥C₁E.

答案：D

5．(2009·山东高考)已知α，β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的　　　　　　　　　　　　　　　 　　　　　　　　　　　　(　)

A．充分不必要条件　　　　　　　 　B．必要不充分条件

C．充要条件 　　　　　　　　　　　D．既不充分也不必要条件

解析：由面面垂直的判定定理可知必要性成立，而当两平面α、β垂直时，α内的直线m只有在垂直于两平面的交线时才垂直于另一个平面β，∴充分性不成立．

答案：B

4．(2010·台州模拟)圆x²+(y+1)²＝3绕直线kx－y－1＝0旋转一周所得的几何体的体积为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　(　)

A．36π 　　　　　B．12π　　　　　　 C．4π 　　　　　　　　　D．4π

解析：显然直线过圆心(0，－1)，故旋转一周所得几何体为球，∴V_球＝πR³＝π·3＝4π.

答案：C