
1.在正方体ABCD-A1B1C1D1中,若E为A1C1中点,则直线CE垂直于 ( )
A.AC B.BD
C.A1D D.A1A
解析:如图所示,易证BD⊥平面AA1C1C,又CE⊂平面ACC1A1,∴BD⊥CE.

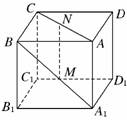 答案:B
答案:B
10.如图是一个几何体的正视图和俯视图.
(1)试判断该几何体是什么几何体;
(2)画出其侧视图,并求该平面图形的面积;
(3)求出该几何体的体积.
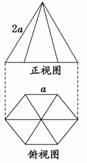
 解:(1)正六棱锥
解:(1)正六棱锥
(2)其侧视图如图:
其中AB=AC,AD⊥BC,
且BC的长是俯视图中正六边形对边的距离,即BC=a,
AD的长是正六棱锥的高,即AD=a,
∴该平面图形的面积
S=a·a=a2.
(3)V=·6·a2·a=a3.
9.如图(1),直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图(2)(3)所示,则其侧视图的面积为________.

解析:其侧视图是底为×2=,高为2的矩形,S=2×=2.
答案:2
8.(2010·枣庄质检)如图,几何体的正视图和侧视图都正确的是 ( )
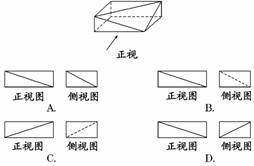
解析:侧视图中,看到一个矩形且不能有实对角线,故A、D排除,而正视图中,应该有一条实对角线,且其对角线位置应为B中所示.
答案:B
7.如图,在斜二测投影下,四边形ABCD是下底角为45°
的等腰梯形,其下底长为5,一腰长为,则原四边
形的面积是________.
 解析:作DE⊥AB于E,CF⊥AB于F,则AE=BF=
解析:作DE⊥AB于E,CF⊥AB于F,则AE=BF=
ADcos45°=1,∴CD=EF=3.将原图复原(如图),则原
四边形应为直角梯形,∠A=90°,AB=5,CD=3,AD
=2,
∴S四边形ABCD=·(5+3)·2=8.
答案:8
|
题组四 |
空间几何体的综合问题 |
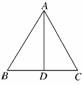
6.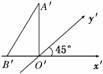 如图所示,△A′O′B′表示水平放置的△AOB的直观图,
如图所示,△A′O′B′表示水平放置的△AOB的直观图,
B′在x′轴上,A′O′和x′轴垂直,且A′O′=2,
则△AOB的边OB上的高为 ( )
A.2 B.4 C.2 D.4
解析:由直观图与原图形中边OB长度不变,
由S原图形=2S直观图,
有·OB·h=2××2·O′B′,∴h=4.
 答案:D
答案:D
5.(2010·盐城模拟)一个几何体的正视图与侧视图都是边长为2的正方形,其俯视图是直径为2的圆,则该几何体的表面积为________.
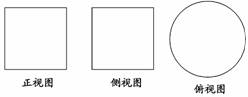
解析:几何体为底面半径为1,母线为2的圆柱,∴S表=S侧+2S底=2π×2+2π=6π.
答案:6π
|
题组三 |
几何体的直观图及斜二测画法 |
4.(2009·福建高考)如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为,则该几何体的俯视图可以是 ( )

解析:∵体积为,而高为1,所以底面为一个直角三角形.
答案:C
3.(2009·合肥模拟)一个空间几何体的三视图及部分数据如图所示,
则这个几何体的体积是 ( )
A.3 B. C.2 D.
 解析:由三视图可知,该几何体为一横放的直三棱柱(如图所示),
解析:由三视图可知,该几何体为一横放的直三棱柱(如图所示),
所以V=×1××=.
答案:D
2.一个无盖的正方体盒子展开后的平面图如图所示,
A、B、C是展开图上的三点,则在正方
体盒子中,∠ABC的大小为 ( )
A.30° B.45° C.60° D.90°
解析:如图所示,将平面图还原为正方体,则AB=BC=CA,
∴∠ABC=60°.
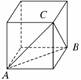
答案:C
|
题组二 |
 几何体的三视图 几何体的三视图 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com