4.在四棱台ABCD－A₁B₁C₁D₁中，上下底面均为正方形，则DD₁与BB₁所在直线是 (　)

A．相交直线 　　　　　　　　　　B．平行直线

C. 不垂直的异面直线　　　　　 　D．互相垂直的异面直线

解析：四棱台可看作是由四棱锥截得的，因此DD₁与BB₁所在直线是相交的．

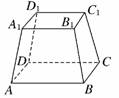
答案：A

3．如图，在四边形ABCD中，已知AB∥CD，直线

AB、BC、AD、DC分别与平面α相交于点E、G、

H、F.

求证：E、F、G、H四点共线(在同一条直线上)．

证明：∵AB∥CD，∴AB、CD确定一个平面β.

又∵AB∩α＝E，AB⊂β，∴E∈α，E∈β，

即E为平面α与β的一个公共点．

同理可证F、G、H均为平面α与β的公共点．

∵两个平面有公共点，它们有且只有一条通过公共点的公共直线，

∴E、F、G、H四点必定共线．

2．对于空间三条直线，有下列四个条件：

①三条直线两两相交且不共点；

②三条直线两两平行；

③三条直线共点；

④有两条直线平行，第三条直线和这两条直线都相交．

其中，使三条直线共面的充分条件有________．

解析：①中两直线相交确定平面，则第三条直线在这个平面内．

②中可能有直线和平面平行．

③中直线最多可确定3个平面．

④同①.

答案：①④

1.如图所示，ABCD－A₁B₁C₁D₁是长方体，O是B₁D₁的中点，

直线A₁C交平面AB₁D_1到于点M，则下列结论正确的是　 (　)

A．A、M、O三点共线

B．A、M、O、A₁不共面

C．A、M、C、O不共面

D．B、B₁、O、M共面

解析：连结A₁C₁，AC，则A₁C₁∥AC，

∴A₁、C₁、C、A四点共面，

∴A₁C⊂平面ACC₁A₁，

∵M∈A₁C，∴M∈平面ACC₁A₁，又M∈平面AB₁D₁，

∴M在平面ACC₁A₁与平面AB₁D₁的交线上，

同理O在平面ACC₁A₁与平面AB₁D₁的交线上，

∴A、M、O三点共线．

答案：A

7．(2009·江西高考改编)如图在四棱锥P－ABCD中，

底面ABCD是矩形，PA⊥平面ABCD，PA＝AD＝4，

AB＝2.以AC的中点O为球心、AC为直径的球面交

PD于点M，交PC于点N.

(1)求证：平面ABM⊥平面PCD；

(2)求直线CD与平面ACM所成的角的正弦值；

解：法一：(1)证明：依题设知，AC是所作球面的直径，

则AM⊥MC.

又因为PA⊥平面ABCD，CD⊂平面ABCD，

∴PA⊥CD.

又CD⊥AD，AD∩PA＝A，所以CD⊥平面PAD，

∵AM⊂平面PAD，∴CD⊥AM，

又CD∩CM＝C，所以AM⊥平面PCD，

∵AM⊂平面ABM，

所以平面ABM⊥平面PCD.

(2)由(1)知，AM⊥PD，又PA＝AD，则M是PD的中点，可得AM＝2且M到平面ABCD的距离为2，

MC＝＝2，

则S_△ACM＝AM·MC＝2，S_△ACD＝4.

设D到平面ACM的距离为h，

由V_D－ACM＝V_M－ACD，即2h＝8，

可求得h＝.

设所求角为θ，则sinθ＝＝，

即直线CD与平面ACM所成角的正弦值为.

法二：(1)同法一；

(2)如图所示，建立空间直角坐标系，

则A(0,0,0)，P(0,0,4)，B(2,0,0)，C(2,4,0)，D(0,4,0)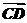，∴＝(－2,0,0)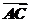，＝(2,4,0)．

由(1)知，AM⊥PD，又PA＝AD，则M是PD的中点，故M(0,2,2)，所以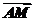＝(0,2,2)．

设平面ACM的一个法向量n＝(x，y，z)，

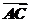由n⊥，n⊥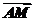，可得令z＝1，

则n＝(2，－1,1)．

设所求角为α，

则sinα＝＝，

所求角的正弦值为.

6．(2010·广州调研)如图，已知等腰直角三角形RBC，

其中∠RBC＝90°，RB＝BC＝2.点A、D分别是

RB、RC的中点，现将△RAD沿着边AD折起到

△PAD位置，使PA⊥AB，连结PB、PC.

(1)求证：BC⊥PB；

(2)求二面角A－CD－P的平面角的余弦值．

解：(1)证明：点A、D分别是RB、RC的中点，

∴AD∥BC，AD＝BC，

∴∠PAD＝∠RAD＝∠RBC＝90°，

∴PA⊥AD，∴PA⊥BC，

∵BC⊥AB，PA∩AB＝A，

∴BC⊥平面PAB.

∵PB⊂平面PAB，∴BC⊥PB.

(2)法一：取RD的中点F，连结AF、PF.

∵RA＝AD＝1，

∴AF⊥RC.

∵AP⊥AR，AP⊥AD，

∴AP⊥平面RBC.

∵RC⊂平面RBC，

∴RC⊥AP.

∵AF∩AP＝A，

∴RC⊥平面PAF.

∵PF⊂平面PAF，

∴RC⊥PF.

∴∠AFP是二面角A－CD－P的平面角．

在Rt△RAD中，AF＝RD＝＝，

在Rt△PAF中，PF＝＝，

cos∠AFP＝＝＝.

∴二面角A－CD－P的平面角的余弦值是.

法二：建立如图所示的空间直角坐标系A－xyz.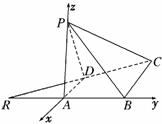

则D(－1,0,0)，C(－2,1,0)，

P(0,0,1)．

∴＝(－1,1,0)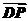，＝(1,0,1)，

设平面PCD的法向量为n＝(x，y，z)，则：

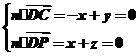令x＝1，得y＝1，z＝－1，

∴n＝(1,1，－1)．

显然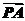，是平面ACD的一个法向量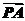，＝(0,0，－1)．

∴cos〈n，〉＝＝＝.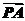

∴二面角A－CD－P的平面角的余弦值是.

5.如图，P－ABCD是正四棱锥，ABCD－A₁B₁C₁D₁是正方体，

其中AB＝2，PA＝.

(1)求证：PA⊥B₁D₁；

(2)求平面PAD与平面BDD₁B₁所成锐二面角的余弦值．

解：以D₁为原点，D₁A₁所在直线为x轴，D₁C₁所在直

线为y轴，D₁D所在直线为z轴建立空间直角坐标系，

则D₁(0,0,0)，A₁(2,0,0)，B₁(2,2,0)，C₁(0,2,0)，

D(0,0,2)，A(2,0,2)，B(2,2,2)，C(0,2,2)，

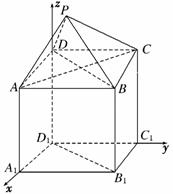P(1,1,4)．

(1)证明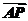：∵＝(－1,1,2)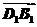，＝(2,2,0)，

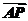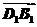∴·＝－2+2+0＝0，

∴PA⊥B₁D₁.

(2)平面BDD₁B₁的法向量为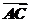＝(－2,2,0)．

＝(2,0,0)，

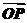＝(1,1,2)．

设平面PAD的法向量为n＝(x，y，z)，则n⊥，n⊥.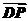

∴　∴取n＝(0，－2,1)，

设所求锐二面角为θ，则

cosθ＝＝＝.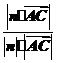

4．(2009·上海高考)如图，在直三棱柱ABC-A₁B₁C₁中，AA₁＝BC＝AB＝2，AB⊥BC，求二面角B₁－A₁C-C₁的大小．

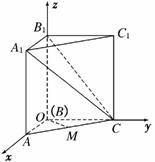
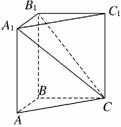
解：如图，建立空间直角坐标系．

则A(2,0,0)，C(0,2,0)，A₁(2,0,2)，B₁(0,0,2)，C₁(0,2,2)，

设AC的中点为M，

∵BM⊥AC，BM⊥CC₁.

∴BM⊥平面A₁C₁C，

即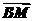＝(1,1,0)是平面A₁C₁C的一个法向量．

设平面A₁B₁C的一个法向量是n＝(x，y，z)．

＝(－2,2，－2)，＝(－2,0,0)，

∴

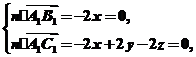
令z＝1，解得x＝0，y＝1.

∴n＝(0,1,1)，

设法向量n与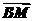的夹角为φ，二面角B₁－A₁C－C₁的大小为θ，显然θ为锐角．

∵cosθ＝|cosφ|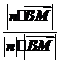＝＝，解得θ＝.

∴二面角B₁－A₁C－C₁的大小为.

题组三

综 合 问 题

3.(2010·陕西八校模拟)在正方体ABCD－A₁B₁C₁D₁中，

M、N分别为棱AA₁和BB₁的中点，则sin

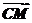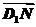〈，〉的值为　　　　　　　　　 (　)

A.　 　　　　　　　　B.

C.　 　　　　　　　D.

解析：设正方体棱长为2，以D为坐标原点，DA为x轴，DC为y轴，DD₁为z轴建立空间直角坐标系，可知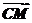＝(2，－2,1)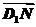，＝(2,2，－1)，

cos〈，〉＝－，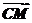

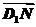sin〈，〉＝.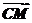

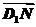答案：B

2．如图，在正方体ABCD－A₁B₁C₁D₁中，棱长为a，

M、N分别为A₁B和AC上的点，A₁M＝AN＝，

则MN与平面BB₁C₁C的位置关系是　　　　　 (　)

A．相交 　　　B．平行　　　　　 C．垂直　　　　 　D．不能确定

解析：∵正方体棱长为a，A₁M＝AN＝，

∴＝，＝，

∴＝++＝++

＝(+)++(+)

＝+.

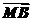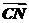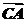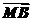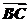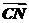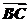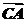
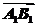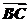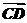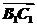又∵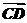是平面B₁BCC₁的法向量，

且·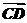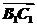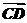＝(+)·＝0，

∴⊥，

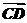∴MN∥平面B₁BCC₁.

答案：B