
8.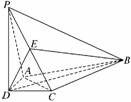 (文)(2009·天津高考)如图,在四棱锥P-ABCD中,
(文)(2009·天津高考)如图,在四棱锥P-ABCD中,
PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为
PC的中点,AD=CD=1,DB=2.
(1)证明PA∥平面BDE;
 (2)证明AC⊥平面PBD;
(2)证明AC⊥平面PBD;
解:(1)证明:设AC∩BD=H,
连结EH.在△ADC中,因为AD=CD,且DB平分
∠ADC,所以H为AC的中点.
又由题设,E为PC的中点,故EH∥PA.
又EH⊂平面BDE且PA⊄平面BDE,
所以PA∥平面BDE.
(2)证明:因为PD⊥平面ABCD,AC⊂平面ABCD,
所以PD⊥AC.
由(1)可得,DB⊥AC.
又PD∩DB=D,
故AC⊥平面PBD.
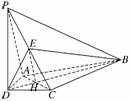
 (理)(2009·北京高考)如图,在三棱锥
(理)(2009·北京高考)如图,在三棱锥
P-ABC中,PA⊥底面ABC,PA=AB,
∠ABC=60°,∠BCA=90°,点D、E
分别在棱PB、PC上,且DE∥BC.
(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(3)是否存在点E使得二面角A-DE-P为直二面角?并说明理由.
解:(1)∵PA⊥底面ABC,∴PA⊥BC.
又∠BCA=90°,∴AC⊥BC,∴BC⊥平面PAC.
(2)∵D为PB的中点,DE∥BC,
∴DE=BC.
又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E,
∴∠DAE是AD与平面PAC所成的角.
∵PA⊥底面ABC,∴PA⊥AB.
又PA=AB,∴△ABP为等腰直角三角形,
∴AD=AB.
在Rt△ABC中,∠ABC=60°,∴BC=AB,
∴在Rt△ADE中,sin∠DAE===,
即AD与平面PAC所成角的正弦值为.
(3)∵DE∥BC,又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC.
又∵AE⊂平面PAC,PE⊂平面PAC,
∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角A-DE-P的平面角.
∵PA⊥底面ABC,∴PA⊥AC,
∴∠PAC=90°,∴在棱PC上存在一点E,使得AE⊥PC.
这时,∠AEP=90°,
故存在点E使得二面角A-DE-P是直二面角.
|
题组四 |
(理)直线与平面所成的角、二面角 |
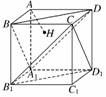
7.如图,正方体AC1的棱长为1,过点A作平面A1BD
的垂线,垂足为点H,则下列命题中错误的是( )
A.点H是△A1BD的垂心
B.AH垂直于平面CB1D1
C.AH的延长线经过点C1
D.直线AH和BB1所成角为45°
解析:因为三棱锥A-A1BD是正三棱锥,故顶点A在底面的射影是底面的中心,A正确;平面A1BD∥平面CB1D1,而AH垂直于平面A1BD,所以AH垂直于平面CB1D1,B正确;根据对称性知C正确.
答案:D
6.(2010·岳阳模拟)设a、b、c表示三条直线,α、β表示两个平面,则下列命题的逆命题不成立的是 ( )
A.c⊥α,若c⊥β,则α∥β
B.b⊂α,c⊄α,若c∥α,则b∥c
C.b⊂β,若b⊥α,则β⊥α
D.b⊂β,c是a在β内的射影,若b⊥c,则b⊥a
解析:C选项的逆命题为b⊂β,若β⊥α则b⊥α.不正确,因为根据平面垂直的性质定理,如果两个平面垂直,其中一个平面内的直线只有垂直交线的才垂直另一个平面.
答案:C
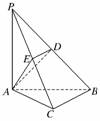
5.(2009·苏北模拟)在四棱锥S-ABCD中,已知AB∥CD,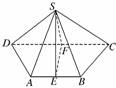
SA=SB,SC=SD,E、F分别为AB、CD的中点.
(1)求证:平面SEF⊥平面ABCD;
(2)若平面SAB∩平面SCD=l,求证:AB∥l.
解:(1)证明:由SA=SB,E为AB中点得SE⊥AB.
由SC=SD,F为CD中点得SF⊥DC.
又AB∥DC,∴AB⊥SF.
又SF∩SE=S,∴AB⊥平面SEF.
又∵AB⊂平面ABCD,
∴平面SEF⊥平面ABCD.
(2)∵AB∥CD,CD⊂面SCD,
∴AB∥平面SCD.
又∵平面SAB∩平面SCD=l,
根据直线与平面平行的性质定理得AB∥l.
|
题组三 |
直线、平面垂直的综合问题 |
4.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,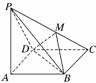
且底面各边都相等,M是PC上的一动点,当点M满足__________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)
解析:由三垂线定理可知,BD⊥PC.
∴当DM⊥PC(或BM⊥PC)时,即有PC⊥平面MBD,而PC⊂平面PCD,∴平面MBD⊥平面PCD.
答案:DM⊥PC(或BM⊥PC等)
3.m、n是空间两条不同的直线,α、β是两个不同的平面,下面四个命题中,真命题的序号是________.
①m⊥α,n∥β,α∥β⇒m⊥n;
②m⊥n,α∥β,m⊥α⇒n∥β;
③m⊥n,α∥β,m∥α⇒n⊥β;
④m⊥α,m∥n,α∥β⇒n⊥β.
解析:①显然正确;②错误,n还可能在β内;③错误,n可能与β相交但不垂直;④正确.
答案:①④
|
题组二 |
平面与平面垂直的判定与性质 |
2.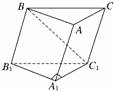 (2010·烟台模拟)如图在斜三棱柱ABC-A1B1C1中,
(2010·烟台模拟)如图在斜三棱柱ABC-A1B1C1中,
∠BAC=90°,BC1⊥AC,则C1在底面ABC上的
射影H必在 ( )
A.直线AB上
B.直线BC上
C.直线AC上
D.△ABC内部
解析:由AC⊥AB,AC⊥BC1,得AC⊥平面ABC1,AC⊂平面ABC,∴平面ABC1⊥平面ABC,C1在面ABC上的射影H必在二平面交线AB上.
答案:A
1.(2010·宣武模拟)若a、b是空间两条不同的直线,α、β是空间的两个不同的平面,则a⊥α的一个充分条件是 ( )
A.a∥β,α⊥β B.a⊂β,α⊥β
C.a⊥b,b∥α D.a⊥β,α∥β
解析:只有选项D,a⊥β,α∥β⇒a⊥α.
答案:D
7.(2009·江西高考)体积为8的一个正方体,其表面积与球O的表面积相等,则球O的体积等于________.
解析:设正方体棱长为a,则a3=8,∴a=2.
∵S正方体=S球,∴6×22=4πR2,∴R= .
V球=πR3=π( )3=.
6.(2009·全国卷Ⅱ)设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C.若圆C的面积等于,则球O的表面积等于________.
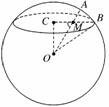 解析:设圆C的半径为r,有πr2=.得r2=.又设球的半径为R,如图所示,有|OB|=R,
解析:设圆C的半径为r,有πr2=.得r2=.又设球的半径为R,如图所示,有|OB|=R,
|OC|=·=R,|CB|=r.
在Rt△OCB中,
有|OB|2=|OC|2+|CB|2,
即R2=R2+r2⇒R2=,
∴R2=2,∴S球=4πR2=8π.
答案:8π
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com