
分析北京空气质量日报,回答15-17题。
|
观测日期 |
北京市各项污染物污染指数 |
||||
|
二氧化硫 |
一氧化碳 |
臭氧 |
二氧化氮 |
可吸入颗粒物 |
|
|
2月16日 |
111 |
77 |
20 |
99 |
138 |
|
3月2日 |
61 |
32 |
19 |
39 |
105 |
|
3月16日 |
32 |
19 |
31 |
22 |
500 |
|
4月2日 |
56 |
32 |
49 |
79 |
260 |
|
4月15日 |
18 |
21 |
32 |
40 |
324 |
|
5月2日 |
37 |
25 |
51 |
44 |
76 |
15.上述与酸雨形成有关的污染物 ( )
A.臭氧 B.二氧化硫
C.一氧化碳 D.可吸人颗粒物
16.这一时期北京大气首要污染物形成的最重要原因是 ( )
①冬季燃煤取暖 ②汽车尾气排放 ③北京春季干旱 ④冷锋活动频繁
A.①② B.③④ C.④② D.①③
17.假如世界大多数国家成为“碳中性国家” (不给地球环境增加二氧化碳负担),对全球产生的影响是 ( )
A.植物的生长速度明显减慢,农作物减产
B.全球平均气温与现在相比大大降低
C.海平面上升速度减缓
D.南北半球的温带草原区更干旱
下图为“某月沿0°经线海平面平均气压分布图”。读图回答12-14题。
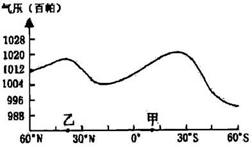
12.上述“某月”是 ( )
A.1月 B.4月 C.7月 D.10月
13.该月份甲地盛行 ( )
A.东南风 B.东北风 C.西南风 D.西北风
14.该月份乙地的气候特征是 ( )
A.高温多雨 B.低温少雨 C.温和多雨 D.炎热干燥
读下图,回答10-11题。
10.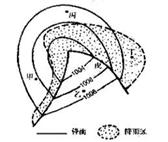 有关图中四地天气状况的正确叙述是 ( )
有关图中四地天气状况的正确叙述是 ( )
A.甲地风向为西南风
B.乙地气温较高
C.丙地风速最大
D.丁地气压最低
11.关于戊地天气系统的正确组合为 ( )
①南半球 ②北半球 ③暖锋 ④冷锋
A.①③ B.②③
C.①④ D.②④
下图为南半球的极地投影示意,据此完成8-9题。
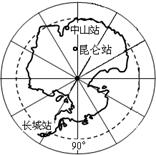
8.南极臭氧洞最容易在南极地区出现的时间是 ( )
A.12月-次年2月 B.3月-5月
C.6 月-8月 D.9月-11月
9.近几十年,长城站附近南极半岛的海岸线变化较大,主要由于 ( )
A.人们的填海造陆 B.强烈地震频繁发生
C.冰架崩裂及消融 D.飓风与风暴潮侵袭
有一则关于长沙的天气资料:前两天天高云淡,气温较低,第三、四天云量逐渐增多,云层加厚,出现连续性降水,第五天雨过天晴,气温升高,气压降低。据此完成6-7题。
6.根据资料分析,长沙的这次降雨类型是 ( )
A.地形雨 B.锋面雨
C.台风雨 D.对流雨
7.影响长沙地区这次降水的天气系统是 ( )
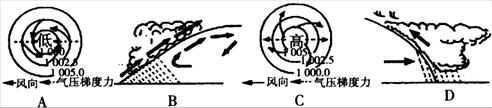
读某区域海平面等压线分布状况模拟示意图,回答3-5题。
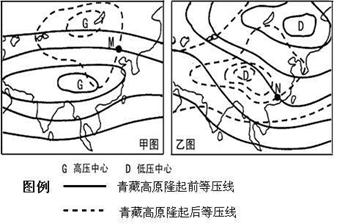
3.气压的分布状况与月份的对应关系最有可能的是 ( )
A.甲图--5月份 B.甲图--1月份
C.乙图--2月份 D.乙图--10月份
4.高原隆起前、后N地的风向是 ( )
A.高原隆起前--东南风 B.高原隆起后--西南风
C.高原隆起前--西南风 D.高原隆起后--西北风
5.高原隆起使M地在图示季节的气候特征出现的变化是 ( )
A.气温降低,降水量减少 B.气温降低,降水量不变
C.气温不变,降水量减少 D.气温增高,降水量增多
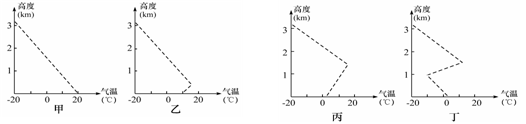 下图是某地气温垂直分布图,读图回答1-2题。
下图是某地气温垂直分布图,读图回答1-2题。
1.甲、乙、丙、丁四图中最有利于大气污染物扩散的是 ( )
A.甲 B.乙
C.丙 D.丁
2.若该地气温由甲逐渐演变到丁,则造成气温垂直变化的原因可能是 ( )
①台风过境 ②晴朗无云的夜晚
③冷空气南下 ④热带海洋气团影响
⑤暖锋过境 ⑥连续阴雨
A.①④ B.③⑥ C.②③ D.⑤⑥
12. 如图所示,四棱锥P-ABCD的底面是边长为
如图所示,四棱锥P-ABCD的底面是边长为
a的正方形,侧棱PA⊥底面ABCD,侧面PBC
内有BE⊥PC于E,且BE=a,试在AB上
找一点F,使EF∥平面PAD.
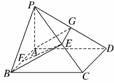 解:在平面PCD内,过E作EG∥CD交PD于G,连结AG,在AB上取点F,使AF=EG,则F即为所求作的点.
解:在平面PCD内,过E作EG∥CD交PD于G,连结AG,在AB上取点F,使AF=EG,则F即为所求作的点.
EG∥CD∥AF,EG=AF,
∴四边形FEGA为平行四边形,
∴FE∥AG.
又AG⊂平面PAD,FE⊄平面PAD,
∴EF∥平面PAD.
又在△BCE中,
CE=
= =a.
在Rt△PBC中,BC2=CE·CP
∴CP==a.又=,
∴EG=AF=a.
∴点F为AB上靠近B的一个三等分点.
11. (2010·徐州模拟)如图所示,四边形ABCD为矩形,
(2010·徐州模拟)如图所示,四边形ABCD为矩形,
BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE.
(1)设点M为线段AB的中点,点N为线段CE的中点.
求证:MN∥平面DAE;
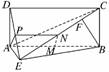 (2)求证:AE⊥BE.
(2)求证:AE⊥BE.
证明:(1)取DE的中点P,连结PA,PN,
因为点N为线段CE的中点,
所以PN∥DC,且PN=DC,
又四边形ABCD是矩形,点M为线段AB的中点,
所以AM∥DC,且AM=DC,
所以PN∥AM,且PN=AM,
故四边形AMNP是平行四边形,
所以MN∥AP.
而AP⊂平面DAE,MN⊄平面DAE,
所以MN∥平面DAE.
(2)因为BC⊥平面ABE,AE⊂平面ABE,
所以AE⊥BC,
又BF⊥平面ACE,AE⊂平面ACE,
所以AE⊥BF,
又BF∩BC=B,
所以AE⊥平面BCE.
又BE⊂平面BCE,
所以AE⊥BE.
10.(2010·昆明模拟)已知m,n是不同的直线,α,β是不重合的平面,给出下列命题:
①若m∥α,则m平行于平面α内的任意一条直线;
②若α∥β,m⊂α,n⊂β,则m∥n;
③若m⊥α,n⊥β,m∥n,则α∥β;
④若α∥β,m⊂α,则m∥β.
上面的命题中,真命题的序号是________.(写出所有真命题的序号)
解析:①由m∥α,则m与α内的直线无公共点,∴m与α内的直线平行或异面.故①不正确.
②α∥β,则α内的直线与β内的直线与无共点,
∴m与n平行或异面,故②不正确.
③④正确.
答案:③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com