
2. 出示例2:课本P116 例3
分析:如何转化为向量问题?进行怎样的向量运算?
1.
出示例1: 如图,在正方体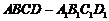 中,E、F分别是
中,E、F分别是 、CD的中点,求证:
、CD的中点,求证: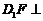 平面ADE.
平面ADE.
证明:不妨设已知正方体的棱长为1个单位 长度,且设
长度,且设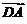 =i,
=i, =j,
=j,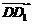 =k.以i、j、k为坐标向量建立空间直角坐标系D-xyz,则
=k.以i、j、k为坐标向量建立空间直角坐标系D-xyz,则
∵ =(-1,0,0),
=(-1,0,0), =(0,
=(0, ,-1),∴
,-1),∴ ·
· =(-1,0,0)·(0,
=(-1,0,0)·(0, ,-1)=0,∴
,-1)=0,∴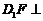 AD.
AD.
又  =(0,1,
=(0,1, ),∴
),∴ ·
· =(0,1,
=(0,1, )·(0,
)·(0, ,-1)=0, ∴
,-1)=0, ∴
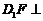 AE.
AE.
又  , ∴
, ∴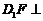 平面ADE.
平面ADE.
说明:⑴“不妨设”是我们在解题中常用的小技巧,通常可用于设定某些与题目要求无关的一些数据,以使问题的解决简单化.如在立体几何中求角的大小、判定直线与直线或直线与平面的位置关系时,可以约定一些基本的长度.⑵空间直角坐标些建立,可以选取任意一点和一个单位正交基底,但具体设置时仍应注意几何体中的点、线、面的特征,把它们放在恰当的位置,才能方便计算和证明.
讨论:将立体几何问题转化为向量问题的途径?
(1)通过一组基向量研究的向量法,它利用向量的概念及其运算解决问题;
(2)通过空间直角坐标系研究的坐标 法,它通过坐标把向量转化为数及其运算来解决问题.
法,它通过坐标把向量转化为数及其运算来解决问题.
第二课时: §3.2立体几何中的向量方法(二)
教学要求:向量运算在几何证明与计算中的应用.掌握利用向量运算解几何题的方法,并能解简单的立体几何问题.
教学重点:向量运算在几何证明与计算中的应用.
教学难点:向量运算在几何证明与计算中的应用.
教学过程:
4. 小结:利用向量解几何题的一般方法:把线段或角度转化为向量表示式,并用已知向量表示未知向量,然后通过向量的运算去计算或证
小结:利用向量解几何题的一般方法:把线段或角度转化为向量表示式,并用已知向量表示未知向量,然后通过向量的运算去计算或证 明.
明.
3. 出示例3:如图,M、N分别是棱长为1的正方 体
体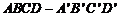 的棱
的棱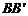 、
、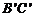 的中点.求异面直线MN与
的中点.求异面直线MN与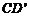 所成的角.
所成的角.
解:∵ =
=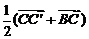 ,
, =
=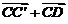 ,
,
∴ =
=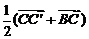 ·
· =
= (
(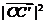 +
+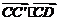 +
+ +
+ )
) .
.
∵ ,
, ,
, ,∴
,∴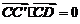 ,
, ,
, ,
,
∴ =
=
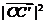 =
= . …求得 cos<
. …求得 cos< >
> ,∴<
,∴< >=
>=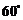 .
.
2. 出示例2:如图,已知线段AB在平面α内,线段
出示例2:如图,已知线段AB在平面α内,线段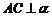 ,线段BD⊥AB,线段
,线段BD⊥AB,线段 ,
, ,如果AB=a,AC=BD=b,求C、D间的距离.
,如果AB=a,AC=BD=b,求C、D间的距离.
解:由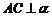 ,可知
,可知 .
.
由 可知,<
可知,<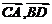 >=
>=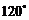 ,
,
∴ =
= =
= +
+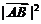 +
+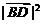 +2(
+2( +
+ +
+ )
)
 =
=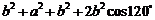 =
=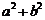 .
.
∴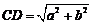 .
.
1. 出示例1:已知空间四边形OABC中, ,
, .求证:
.求证: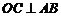 .
.
 证明:
证明: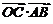 =
=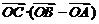 =
= -
-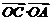 .
.
∵ ,
, , ∴
, ∴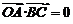 ,
, ,
,
 ,
,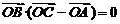 .
.
∴ ,
, .
.
∴ =
=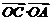 ,
,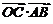 =0. ∴
=0. ∴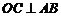
2. 通法分析:利用两个向量的数量积的定义及其性质可以解决哪些问题呢?
⑴利用定义a·b=|a||b|cos<a,b>或cos<a,b>=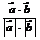 ,可求两个向量的数量积或夹角问题;
,可求两个向量的数量积或夹角问题;
⑵利用性质a⊥b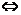 a·b=0可以解决线段或直线的垂直问题;
a·b=0可以解决线段或直线的垂直问题;
⑶利用性质a·a=|a|2,可以解决线段的长或两点间的距离问题.
1. 用向量解决立体几何中的一些典型问题的基本思考方法是:⑴如何把已知的几何条件(如线段、角度等)转化为向量表示; ⑵考虑一些未知的向量能否用基向量或其他已知向量表式; ⑶如何对已经表示出来的向量进行运算,才能获得需要的结论?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com