
2. 变式: 用向量法求:二面角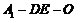 余弦;OF与DE的距离;O点到平面DEF的距离.
余弦;OF与DE的距离;O点到平面DEF的距离.
1. 出示例1:长方体
出示例1:长方体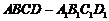 中,AD=
中,AD=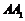 =2,AB=4,E、F分别是
=2,AB=4,E、F分别是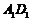 、AB的中点,O是
、AB的中点,O是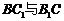 的交点. 求直线OF与平面DEF所成角的正弦.
的交点. 求直线OF与平面DEF所成角的正弦.
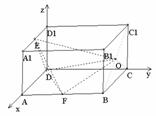
解:以点D为空间直角坐标系的原点,DA、DC、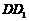 为坐标轴,建立如图所示的空间直角坐标
为坐标轴,建立如图所示的空间直角坐标 系. 则
系. 则
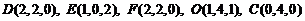 .
.
设平面DEF的法向量为 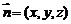 ,
,
则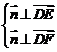 , 而
, 而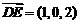 ,
, 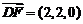 .
.
∴ 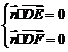 ,即
,即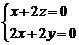 , 解得
, 解得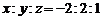 , ∴
, ∴ 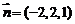 .
.
∵ 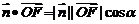 , 而
, 而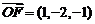 .
.
∴ 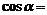
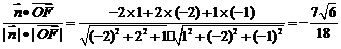
所以,直线OF与平面DEF所成角的正弦为 .
.
3. 讨论:如何利用向量求空间距离?
两异面直线的距离,转化为与两异面直线都相交的线段在公垂向量上的投影长.
点到平面的距离,转化为过这点的平面的斜线在平面的法向量上的投影长.
2. 讨论:如何利用法向量求线面角? → 面面角?
直线AB与平面α所成的角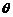 ,可看成是向
,可看成是向 量
量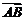 所在直线与平面α的法向量
所在直线与平面α的法向量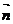 所在直线夹角的余角,
所在直线夹角的余角, 从而求线面角转化为求直线所在的向量与平面的法向量的所成的线线角,根据两个向量所成角的余弦公式
从而求线面角转化为求直线所在的向量与平面的法向量的所成的线线角,根据两个向量所成角的余弦公式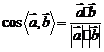 ,我们可以得到如下向量法的公式:
,我们可以得到如下向量法的公式:
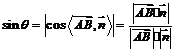 .
.
1. 法向量定义:如果直线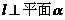 , 取直线l的方向向量为
, 取直线l的方向向量为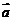 ,则向量
,则向量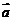 叫作平面α的法向量(normal vec
叫作平面α的法向量(normal vec tors). 利用法向量,可以巧妙的解决空间角度和距离.
tors). 利用法向量,可以巧妙的解决空间角度和距离.
第三课时: §3.2立体几何中的向量方法(三)
教学要求:向量运算在几何证明与计算中的应用.掌握利用向量运算解几何题的方法,并能解简单的立体几何问题.
教学重点:向量运算在几何证明与计算中的应用.
教学难点:向量运算在几何证明与计算中的应用.
教学过程:
6. 小结:
向量法解题“三步曲”:(1)化为向量问题 →(2)进行向量运算 →(3)回到图形问题.
5. 法向量定义:如果表示向量a的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作a⊥α.如果a⊥α,那么向量a叫做平面α的法向量.
4. 出示例4:证:如果两条直线同垂直于一个平面,则这两条直线平行.
改写为:已知:直线OA⊥平面α,直线BD⊥ 平面α,O、B为垂足.求证:OA//BD.
平面α,O、B为垂足.求证:OA//BD.
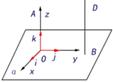 证明:以点O为原点,以射线OA为非负z轴,建立空间直角坐标系O-xyz,i,j,k为沿x轴,y轴,z轴的坐标向量,且设
证明:以点O为原点,以射线OA为非负z轴,建立空间直角坐标系O-xyz,i,j,k为沿x轴,y轴,z轴的坐标向量,且设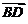 =
=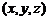 .
.
∵BD⊥α, ∴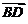 ⊥i,
⊥i,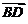 ⊥j,
⊥j,
∴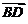 ·i=
·i=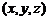 ·(1,0,0)=x=0,
·(1,0,0)=x=0,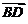 ·j=
·j=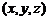 ·(0,1,0)=y=0,
·(0,1,0)=y=0,
∴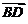 =(0,0,z).∴
=(0,0,z).∴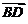 =zk.即
=zk.即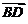 //k.由已知O、B为两个不同的点,∴OA//BD.
//k.由已知O、B为两个不同的点,∴OA//BD.
3. 出示例3:课本P118 例4
分析:如何转化为向量问题?进行怎样的向量运算?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com