
22. 已知椭圆 (a>b>0)的离心率为
(a>b>0)的离心率为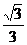 ,过右焦点F的直线
,过右焦点F的直线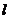 与椭圆C相交于AB两点,当
与椭圆C相交于AB两点,当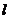 斜率为1时,坐标原点O到
斜率为1时,坐标原点O到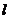 的距离为
的距离为
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有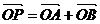 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
21. 若数列 的前
的前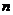 项和
项和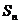 是
是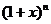 二项展开式中各项系数的和
二项展开式中各项系数的和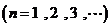 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若数列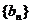 满足
满足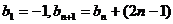 ,且
,且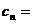
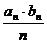 ,求数列
,求数列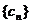 的通项及其前
的通项及其前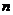 项和
项和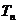 。
。
20.已知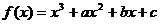 的图像与y轴交于点(0,2),
的图像与y轴交于点(0,2),
并且在x=1处切线的方向向量为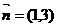 。
。
(1)若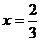 是函数
是函数 的极值点,求
的极值点,求 的解析式;
的解析式;
(2)若函数 在区间[
在区间[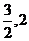 ]单调递增,求实数b的取值范围。
]单调递增,求实数b的取值范围。
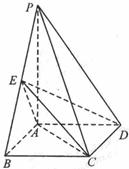
19.如图,四棱锥P-ABCD中,底面ABCD为矩形,
PA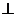 底面ABCD,PA=AB=
底面ABCD,PA=AB=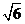 ,点E是棱PB的中点。
,点E是棱PB的中点。
(1)AD与平面PBC的距离;
(2)若AD= ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。
18.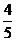 公安机关交通管理部门规定,获取《机动车驾驶证》必须依次参加交管部门组织的“理论”“倒桩”“考场”和“路考”四个科目的考试,前一科目考试合格才能参加后一科目考试,且每个科目考试都合格才能获得《机动车驾驶证。已知某人参加考试能一次性通过各科目的概率均为
,且各科目考试能否通过互不影响。
公安机关交通管理部门规定,获取《机动车驾驶证》必须依次参加交管部门组织的“理论”“倒桩”“考场”和“路考”四个科目的考试,前一科目考试合格才能参加后一科目考试,且每个科目考试都合格才能获得《机动车驾驶证。已知某人参加考试能一次性通过各科目的概率均为
,且各科目考试能否通过互不影响。
(1)求该人进入“路考”科目考试且该科目考试不合格的概率;
 (2)求该人至多进入“倒桩”科目考试的概率.
(2)求该人至多进入“倒桩”科目考试的概率.
17.17.已知向量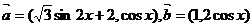 ,设函数
,设函数 。
。
(1)求 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)在△ABC中,角A、B、C所对的边分别为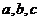 ,若
,若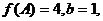 △ABC面积为
△ABC面积为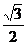 ,求
,求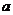 的值。
的值。
16.对于下列命题:
①已知集合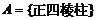 ,
,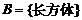 ,则
,则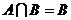 ;
;
②函数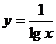 在
在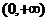 为单调函数;
为单调函数;
③在平面直角坐标系内,点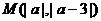 与
与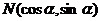 在直线
在直线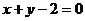 的异侧;
的异侧;
④若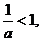 则
则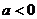 或
或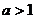 ;
;
⑤互为反函数的两个不同函数的图象若有交点,则交点一定在直线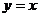 上。其中正确命题的序号为 。(写出所有正确命题的序号)
上。其中正确命题的序号为 。(写出所有正确命题的序号)
15.在半径为R的球面上有不同的三个点A、B、C,已知A、B、C三点中任意两点的球面距离均为 ,O为球心,则三棱锥 O-ABC的体积 。
,O为球心,则三棱锥 O-ABC的体积 。
14.学校为研究男女同学数学学习的差异情况,对某班60名同学(其中男同学15名,女同学45名)采取分层抽样的方法,抽取一个样本容量为10的样本进行研究,女同学甲被抽到的概率为 。
13.二项式 的展开式中的常数项为 。 (用数字作答)
的展开式中的常数项为 。 (用数字作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com