
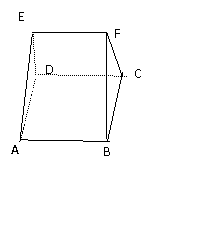
6、如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,
EF//AB, EF=3/2,EF与面AC的距离为2,则该多面体的体积为……( )
A)9/2 B)5 C)6 D)15/2
5、方程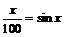 的实数解的个数为 ( )
的实数解的个数为 ( )
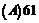
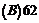
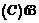

4、若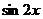 、
、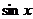 分别是
分别是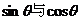 的等差中项和等比中项,则
的等差中项和等比中项,则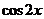 的值为:( )
的值为:( )
 A、
A、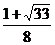 B、
B、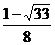 C、
C、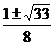 D、
D、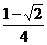
3、已知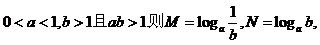
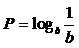 .三数大小关系为 ( )
.三数大小关系为 ( )
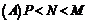

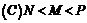
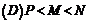
1、若sin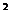 x>cos
x>cos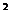 x,则x的取值范围是(
)
x,则x的取值范围是(
)
(A){x|2k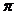 -
-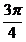 <x<2k
<x<2k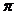 +
+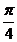 ,k
,k Z} (B) {x|2k
Z} (B) {x|2k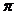 +
+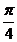 <x<2k
<x<2k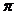 +
+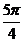 ,k
,k Z}
Z}
(C) {x|k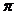 -
-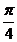 <x<k
<x<k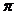 +
+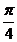 ,k
,k Z } (D) {x|k
Z } (D) {x|k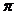 +
+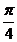 <x<k
<x<k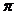 +
+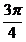 ,k
,k Z}
Z}
2 在复平面内,把复数3-
在复平面内,把复数3-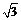 i对应的向量按顺时针方向旋转π/3,所得向量对应的复数是…………………………( )
i对应的向量按顺时针方向旋转π/3,所得向量对应的复数是…………………………( )
A)2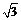 B)-2
B)-2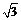 i C)
i C)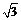 -3i D)3+
-3i D)3+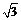 i
i
10.某人乘坐出租车从A地到乙地,有两种方案:第一种方案,乘起步价为10元,每km价1.2元的出租车;第二种方案,乘起步价为8元,每km价1.4元的出租车,按出租车管理条例,在起步价内,不同型号的出租车行驶的里路是相等的,则此人从A地到B地选择哪一种方案比较适合?
解:设A地到B地距离为mkm,起步价内行驶的路为akm
显然,当m≤a时,选起步价为8元的出租车比较合适
当m>a时,设m=a+x(x>0),乘坐起步价为10元的出租车费用为P(x)元,乘坐起步价为8元的出租车费用为Q(x)元,则P(x)=10+1.2x,Q(x)=8+1.4x
∵ P(x)-Q(x)=2-0.2x=0.2(10-x)
∴ 当x>10时,P(x)<Q(x),此时起步价为10元的出租车比较合适
当x<10时,P(x)>Q(x),此时选起步价为8元的出租车比较合适
当x=10时,P(x)=Q(x),此时两种出租车任选
[探索题]设关于x的方程2x2-ax-2=0的两根为α、β(α<β),函数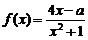 .
.
(Ⅰ)求f (α)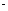 f (β)的值;
f (β)的值;
(Ⅱ)证明f (x)是[α,β]上的增函数;
(Ⅲ)当a为何值时,f (x)在区间[α,β]上的最大值与最小值之差最小?
解:(Ⅰ)由题意知α+β=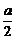 ,α·β=-1,∴α2+β2=
,α·β=-1,∴α2+β2=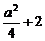 ,
,
f
(α)·f (β)=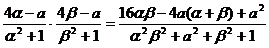
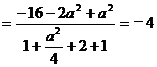 .
.
(Ⅱ)证明:设α≤x1<x2≤β,
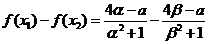
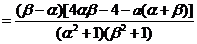
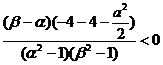
所以f(x)在[α,β]在是增函数.
(法2:导数法)
(Ⅲ)f (x)在区间[α,β]上的最大值f (β)>0,最小值f (α)<0,
又∵| f (α)·f (β) |=4,
∴f
(β)-f (α)=|
f (β)|+| f
(α)|≥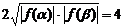
当且仅当| f (β)|=| f (α)|=2时取“=”号,此时f (β)=2,f (α)=-2
∴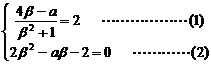
由(1)、(2)得 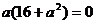 ,∴a=0为所求。
,∴a=0为所求。
9.用一块矩形木板紧贴一墙角围成一直三棱柱空间堆放谷物,已知木板的长为a,宽为b,墙角的两堵墙面和地面两两互相垂直,怎样围法,使直三棱柱的空间最大?这个最大值是多少?
解:如图:A-CC1---B是二墙面所成直二面角, CC1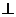 面ABC
面ABC
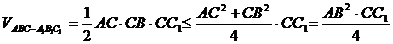 (AC=CB时取”=”)
(AC=CB时取”=”)
当AB=a,AA1=b时,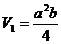
当AB=b,AA1=a时,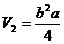
8. (2004全国IV)已知数列{an}的前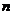 项和Sn满足
项和Sn满足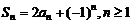 .
.
(1)写出数列{an}的前三项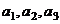 ;
;
(2)求数列{an}的通项公式;
(3)证明:对任意的整数m>4,有
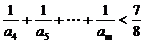 .
.
(Ⅰ)解:由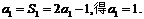
由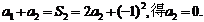
由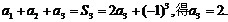
(Ⅱ)解:当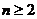 时,有
时,有
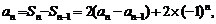
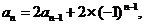
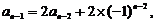 ……
……
 所以
所以
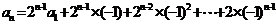
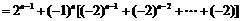
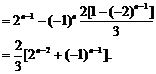
经验证a1也满足上式,所以
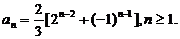
(Ⅲ)证明:
记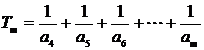
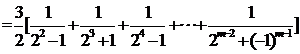
(想用放缩法)
注意到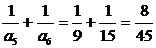
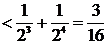 . 一般地
. 一般地
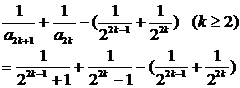
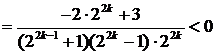
即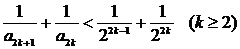
∴当m是奇数时,
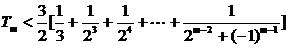
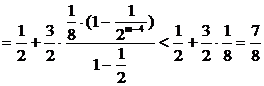
当m是偶数时,再添上第m+1项(放大了)凑够奇数项,利用上述结论可知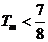 也成立,
也成立,
所以对任意整数m>4,有
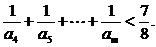
7. (2003福建质检)已知函数f(x)=|log2(x+1)|,实数m、n在其定义域内,且m<n,f(m)=f(n).
求证:(1)m+n>0;
(2)f(m2)<f(m+n)<f(n2).
(1)证法一:由f(m)=f(n),得|log2(m+1)|=|log2(n+1)|,即log2(m+1)=±log2(n+1),
log2(m+1)=log2(n+1), ①
或log2(m+1)=log2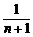 . ②
. ②
由①得m+1=n+1,与m<n矛盾,舍去.
由②得m+1=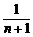 ,即(m+1)(n+1)=1. ③
,即(m+1)(n+1)=1. ③
∴m+1<1<n+1.∴m<0<n.∴mn<0.
由③得mn+m+n=0,m+n=-mn>0.
证法二:(同证法一得)(m+1)(n+1)=1.
∵0<m+1<n+1,∴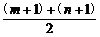 >
>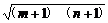 =1.∴m+n+2>2.∴m+n>0.
=1.∴m+n+2>2.∴m+n>0.
(2)证明:当x>0时,f(x)=|log2(x+1)|=log2(x+1)在(0,+∞)上为增函数.
由(1)知m2-(m+n)=m2+mn=m(m+n),且m<0,m+n>0,∴m(m+n)<0.
∴m2-(m+n)<0,0<m2<m+n.
∴f(m2)<f(m+n).
同理,(m+n)-n2=-mn-n2=-n(m+n)<0,
∴0<m+n<n2.∴f(m+n)<f(n2).
∴f(m2)<f(m+n)<f(n2).
6.设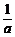 +
+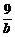 =1,a、b∈N*,则a=
=1,a、b∈N*,则a=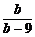 .
.
∴a+b=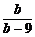 +b,b>9时,
+b,b>9时,
a+b=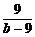 +b-9+10≥16.
+b-9+10≥16.
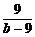 =b-9,即b=12取等号,此时a=4.
=b-9,即b=12取等号,此时a=4.
b<9无解.∴a=4,b=12.答案:4 12
[解答题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com