
2.分式不等式,切忌去分母,一律移项通分化为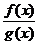 >0(或
>0(或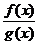 <0)的形式,转化为:
<0)的形式,转化为: ,即转化
,即转化
为一次、二次或特殊高次不等式形式 .
也可以直接用根轴法(零点分段法)求解
1.特殊的高次不等式即右边化为0,左边可分解为一次或二次式的因式的形式不等式,一般用区间法解,注意:①左边各因式中x的系数化为“+”,若有因式为二次的(不能再分解了)二次项系数也化为“+”,再按我们总结的规律作;②注意边界点(数轴上表示时是“0”还是“.”).
⒈ 一元二次不等式与特殊的高次不等式解法
例1 解不等式 .
.
分析一:利用前节的方法求解;
分析二:由乘法运算的符号法则可知,若原不等式成立,则左边两个因式必须异号,∴原不等式的解集是下面两个不等式组: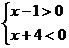 与
与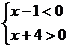 的解集的并集,即{x|
的解集的并集,即{x|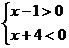 }∪
}∪ }=φ∪{x|-4<x<1}={x|-4<x<1}.书写时可按下列格式:
}=φ∪{x|-4<x<1}={x|-4<x<1}.书写时可按下列格式:
解二:∵(x-1)(x+4)<0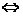
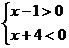 或
或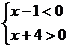
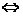 x∈φ或-4<x<1
x∈φ或-4<x<1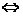 -4<x<1,
-4<x<1,
∴原不等式的解集是{x|-4<x<1}.
小结:
一元二次不等式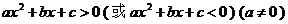 的代数解法:设一元二次不等式
的代数解法:设一元二次不等式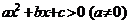 相应的方程
相应的方程
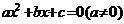 的两根为
的两根为 ,
,
则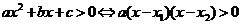 ;
;
①若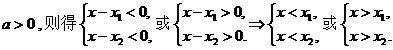
当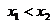 时,得
时,得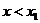 或
或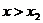 ;当
;当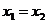 时,得
时,得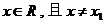 .
.
②若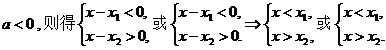
当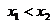 时,得
时,得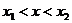 ;当
;当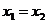 时,得
时,得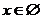 .
.
分析三:由于不等式的解与相应方程的根有关系,因此可求其根并由相应的函数值的符号表示出来即可求出不等式的解集.
解:①求根:令(x-1)(x+4)=0,解得x(从小到大排列)分别为-4,1,这两根将x轴分为三部分:(- ,-4)(-4,1)(1,+
,-4)(-4,1)(1,+ );
);
②分析这三部分中原不等式左边各因式的符号
|
|
(- ,-4) ,-4) |
(-4,1) |
(1,+ ) ) |
|
x+4 |
- |
+ |
+ |
|
x-1 |
- |
- |
+ |
|
(x-1)(x+4) |
+ |
- |
+ |
③由上表可知,原不等式的解集是{x|-4<x<1}.
例2:解不等式:(x-1)(x+2)(x-3)>0;
解:①检查各因式中x的符号均正;
②求得相应方程的根为:-2,1,3;
③列表如下:
|
|
-2 1 3 |
|||
|
x+2 |
- |
+ |
+ |
+ |
|
x-1 |
- |
- |
+ |
+ |
|
x-3 |
- |
- |
- |
+ |
|
各因式积 |
- |
+ |
- |
+ |
④由上表可知,原不等式的解集为:{x|-2<x<1或x>3}.
小结:此法叫列表法,解题步骤是:
①将不等式化为(x-x1)(x-x2)…(x-xn)>0(<0)形式(各项x的符号化“+”),令(x-x1)(x-x2)…(x-xn)=0,求出各根,不妨称之为分界点,一个分界点把(实数)数轴分成两部分,n个分界点把数轴分成n+1部分……;
②按各根把实数分成的n+1部分,由小到大横向排列,相应各因式纵向排列(由对应较小根的因式开始依次自上而下排列);
③计算各区间内各因式的符号,下面是乘积的符号;
④看下面积的符号写出不等式的解集.
练习:解不等式:x(x-3)(2-x)(x+1)>0. {x|-1<x<0或2<x<3}.
 思考:由函数、方程、不等式的关系,能否作出函数图像求解
思考:由函数、方程、不等式的关系,能否作出函数图像求解
直接写出解集:{x|-2<x<1或x>3}. {x|-1<x<0或2<x<3}
在没有技术的情况下:
可大致画出函数图形求解,称之为根轴法(零点分段法)
①将不等式化为(x-x1)(x-x2)…(x-xn)>0(<0)形式,并将各因式x的系数化“+”;(为了统一方便)
②求根,并在数轴上表示出来;
③由右上方穿线,经过数轴上表示各根的点(为什么?);
④若不等式(x的系数化“+”后)是“>0”,则找“线”在x轴上方的区间;若不等式是“<0”,则找“线”在x轴下方的区间.

注意:奇过偶不过
例3 解不等式:(x-2)2(x-3)3(x+1)<0.
解:①检查各因式中x的符号均正;
②求得相应方程的根为:-1,2,3(注意:2是二重根,3是三重根);
③在数轴上表示各根并穿线,每个根穿一次(自右上方开始奇过偶不过),如下图: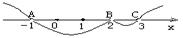
④∴原不等式的解集为:{x|-1<x<2或2<x<3}.
说明:∵3是三重根,∴在C处过三次,2是二重根,∴在B处过两次,结果相当于没过.由此看出,当左侧f(x)有相同因式(x-x1)n时,n为奇数时,曲线在x1点处穿过数轴;n为偶数时,曲线在x1点处不穿过数轴,不妨归纳为“奇过偶不过”.
练习:解不等式:(x-3)(x+1)(x2+4x+4)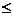 0.
0.
解:①将原不等式化为:(x-3)(x+1)(x+2)2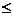 0;
0;
②求得相应方程的根为:-2(二重),-1,3;
③在数轴上表示各根并穿线,如图:
④∴原不等式的解集是{x|-1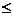 x
x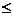 3或x=-2}.
3或x=-2}.
说明:注意不等式若带“=”号,点画为实心,解集边界处应有等号;另外,线虽不穿过-2点,但x=-2满足“=”的条件,不能漏掉.
2.分式不等式的解法
例4 解不等式: .
.
错解:去分母得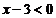 ∴原不等式的解集是
∴原不等式的解集是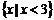 .
.
解法1:化为两个不等式组来解:
∵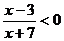
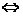
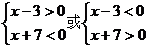
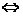 x∈φ或
x∈φ或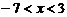
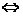
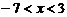 ,
,
∴原不等式的解集是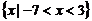 .
.
解法2:化为二次不等式来解:
∵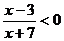
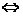
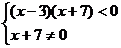
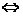
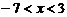 ,
,
∴原不等式的解集是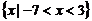
说明:若本题带“=”,即(x-3)(x+7)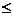 0,则不等式解集中应注意x
0,则不等式解集中应注意x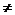 -7的条件,解集应是{x| -7<x
-7的条件,解集应是{x| -7<x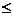 3}.
3}.
小结:由不等式的性质易知:不等式两边同乘以正数,不等号方向不变;不等式两边同乘以负数,不等号方向要变;分母中有未知数x,不等式两边同乘以一个含x的式子,它的正负不知,不等号方向无法确定,无从解起,若讨论分母的正负,再解也可以,但太复杂.因此,解分式不等式,切忌去分母.
解法是:移项,通分,右边化为0,左边化为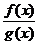 的形式.
的形式.
例5 解不等式: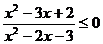 .
.
解法1:化为不等式组来解较繁.
解法2:∵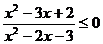
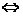
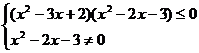
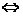
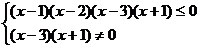 ,
,
∴原不等式的解集为{x| -1<x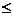 1或2
1或2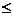 x<3}.
x<3}.
也可以直接用根轴法(零点分段法)求解: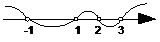
练习:1.课本P21练习:3⑴⑵;2.解不等式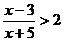 .
.
答案:1.⑴{x|-5<x<8};⑵{x|x<-4,或x>-1/2};2.{x|-13<x<-5}.
2解不等式: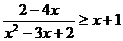 .(答:{x|x
.(答:{x|x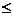 0或1<x<2})
0或1<x<2})
2.一元二次不等式的解法步骤
一元二次不等式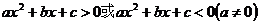 的解集:
的解集:
设相应的一元二次方程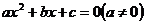 的两根为
的两根为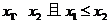 ,
,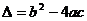 ,则不等式的解的各种情况如下表:(课本第19页)
,则不等式的解的各种情况如下表:(课本第19页)
|
|
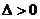 |
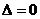 |
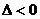 |
|
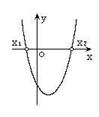
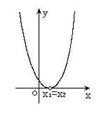
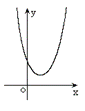
二次函数 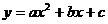 ( 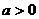 )的图象 )的图象 |
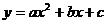  |
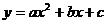  |
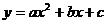  |
一元二次方程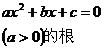 |
有两相异实根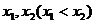 |
有两相等实根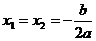 |
无实根 |
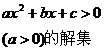 |
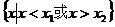 |
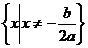 |
R |
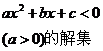 |
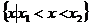 |
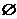 |
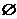 |
引言:今天我们来研究一元二次不等式的另外解法,以及特殊的高次不等式、分式不等式的解法
1.一元二次方程、一元二次不等式与二次函数的关系
21.已知固体化合物A由NaHCO3、KHCO3、MgCO3、CaCO3四种物质中的两种混合而成。请通过计算和推理回答下列问题:[n(A)表示A的物质的量;m(A)表示A的质量]
(1)取A与足量的盐酸反应:若m(A)为定值,生成气体的量即为定值,试写出A的可能组成,并用简单的语言说明你判断的理由。
(2)若先将A加热,剩余固体再与足量的盐酸反应,且先后两次产生的气体分别通入足量的澄清石灰水,生成的沉淀均为10.0g,据此推导出A的组成及物质的量。
20.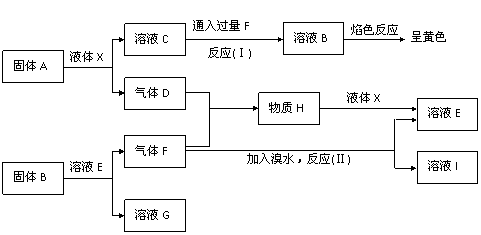 在一定条件下,下列各物质可发生如下图所示的变化(反应中生成的水没有写出),请回答有关问题。
在一定条件下,下列各物质可发生如下图所示的变化(反应中生成的水没有写出),请回答有关问题。
(1)固体A的电子式为__________________,B的化学式为____________。
(2)分别写出反应(Ⅰ)、(Ⅱ)的离子方程式:
Ⅰ______________________________、Ⅱ______________________________。
(3)气体F在一定条件下可被固体A完全吸收,该反应的化学方程式为:
___________________________________________________________。
19.(8分)有A、B、C、D四种短周期元素,它们的原子序数由A到D依次增大,已知A和B原子有相同的电子层数,且A的最外层电子数是次外层电子数的两倍;C的单质燃烧时呈现黄色火焰,C的单质在加热条件下与B的单质反应,可以得到与D单质颜色相同的固态化合物甲;D的最高价与最低价代数和为其最低价绝对值的两倍。据此,回答下列问题:
(1)写出A与B两元素所形成化合物AB2的电子式__________,该化合物分子属于
分子(极性或非极性)。
(2)用电子式表示形成C2D的形成过程: 。
(3)C、D两元素还可以形成化合物C2D2,该化合物性质类似于C2B2,试写出C2D2与稀盐酸反应的化学方程式 。
18.已知碱金属的氧化物有:普通氧化物,如Li2O;过氧化物,如Na2O2;超氧化物,如KO2;臭氧化物,如RbO3,其中后三者均能与H2O或CO2反应产生O2 。
(1)宇航工业,为了能保持飞船座舱内空气成分的稳定,宇航科学家进行了大量的探索,有的科学家提出了“金属过氧化物处理系统”。即不断把座舱内的空气通过盛有金属过氧化物(以过氧化钠为例)的容器,并把处理后的气体充入座舱。每个宇航员平均每天需要消耗0.9 kg氧气,呼出1.0 kg二氧化碳。有关反应的化学方程式为 、 ;将处理后的气体充入座舱时,为了能保持飞船座舱内空气成分的稳定,还应采取的措施是___________________________________。
(2)人体内O2-离子对健康有害,使人过早衰老,但在催化剂SOD存在下可发生如下反应,请完成该反应的离子方程式: O2- + H2O = H2O2+ O2+
 (3)Na2O2、K2O2、CaO2以及BaO2都可与酸作用生成过氧化氢,
(3)Na2O2、K2O2、CaO2以及BaO2都可与酸作用生成过氧化氢,
目前实验室制取过氧化氢可通过上述某种过氧化物与适量
稀硫酸作用,过滤即可制得。最适合的过氧化物是
(写电子式)
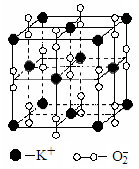
(4)高温下,超氧化钾晶体呈立方体结构。晶体中氧的化
合价部分为0价,部分为-2价。如图为超氧化钾晶体
的一个晶胞(晶体中最小的重复单元)。则每个超氧
化钾晶胞含有 个K+和 个O2-;该晶体中,
0价氧原子与-2价氧原子的数目比为
17.某未知溶液X中可能含有K+、Fe2+、NH4+、Cl-。检验其中是否含有K+,通常有如下两套实验方案。
方案一:焰色反应法
用洁净的玻璃棒蘸取未知液X置于酒精灯外焰上灼烧,观察到火焰呈黄色,则证明其中不含K+。对上述实验过程中的错误和疏漏之处加以纠正、补充:
、 。
方案二:亚硝酸钴钠法
在CH3COOH酸化的溶液中,K+与亚硝酸钴钠[Na3Co(NO2)6]反应生成黄色沉淀[K2NaCo(NO2)6],该原理可用于K+的检验。注意:NH4+也能与Na3Co(NO2)6生成黄色沉淀,会干扰K+离子的检验。
请你利用上述反应原理设计一个实验方案,检验未知溶液X中是否含有K+。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com