4. 空间向量数量积的运算律：与平面向量的数量积一样，空间向量的数量积有如下运算律：

⑴(λa)·b＝λ(a·b)＝a·(λb)　 (数乘结合律)；　⑵ a·b＝b·a　 (交换律)；

　⑶a·(b+c)＝a·b+a·c　 (分配律)

说明：⑴(a·b)c≠a(b·с)；⑵有如下常用性质：a²＝｜a｜²，(a+b)²＝a²+2a·b+b^2[来源:]

3. 空间数量积的性质：根据定义，空间向量的数量积和平面向量的数量积一样，具有以下性质：

　⑴a·e＝｜a｜·cos＜a,e＞；　⑵a⊥b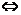a·b＝0

　⑶当a与b同向时，a·b＝｜a｜·｜b｜；　当a与b反向时，a·b＝－｜a｜·｜b｜.

　特别地，a·a＝｜a｜²或｜a｜＝.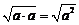

　⑷cos＜a,b＞＝;　⑸｜a·b｜≤｜a｜·｜b｜.

2. 两个向量的数量积：已知空间两个向量a与b，|a||b|cos＜a、b＞叫做向量a、b的数量积，记作a·b，即　a·b＝|a||b|cos＜a,b＞.

说明：⑴零向量与任一向量的数量积为0，即0·a＝0；

⑵符号“· ”在向量运算中不是乘号，既不能省略，也不能用“×”代替.

几何意义：已知向量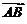＝a和轴l，e是l上和l同方向的单位向量．作点A在l上的射影A′，点B在l上的射影B′，则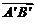叫做向量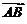在轴l上或在e方向上的正射影，简称射影．可以证明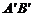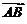：＝｜｜cos＜a,e＞＝a·e．说明：一个向量在轴上的投影的概念，就是a·e的几何意义．

1. 两个非零向量夹角的概念：已知两个非零向量a与b，在空间中任取一点O，作＝a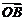，＝b，则∠AOB叫做向量a与b的夹角，记作＜a,b＞．

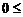说明：⑴规定：＜a，b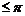＞．　当＜a、b＞＝0时，a与b同向；　当＜a、b＞＝π时，a与b反向；

　当＜a、b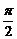＞＝时，称a与b垂直，记a⊥b．

⑵ 两个向量的夹角唯一确定且＜a,b＞＝＜b,a＞．

⑶ 注意：①在两向量的夹角定义中，两向量必须是同起点的．

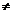　　②＜a,b＞(a,b)

2. 平面向量中有两个平面向量的数量积，与其类似，空间两个向量也有数量积.

2. 作业：课本P₉₆　 练习2题.

第四课时3.1.3空间向量的数量积运算

教学要求：掌握空间向量夹角和模的概念及表示方法；掌握两个向量数量积的概念、性质和计算方法及运算律；掌握两个向量数量积的主要用途，会用它解决立体几何中的一些简单问题.

教学重点：两个向量的数量积的计算方法及其应用．

教学难点：向量运算在几何证明与计算中的应用．

教学过程：

1. 练习：课本P₉₆　 练习3题.

7. 例题：课本P₉₅例1 ，解略． → 小结：向量方法证明四点共面

6. 共面向量定理的推论是：空间一点P在平面MAB内的充要条件是存在有序实数对x，y，使得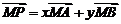，① 或对于空间任意一定点O，有　 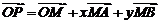．②

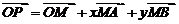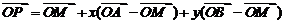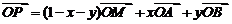分析：⑴推论中的x、y是唯一的一对有序实数；　 ⑵由得：， ∴ ③

公式①②③都是P、M、A、B四点共面的充要条件．