
6.
练习:已知a= ,b=
,b= ,求a+b,a-b,8a,a·b.解:略.
,求a+b,a-b,8a,a·b.解:略.
5.
两个向量共线或垂直的判定:设a= ,b=
,b= ,则
,则
⑴a//b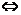 a=λb
a=λb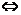
 ,
,
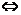
 ;
;
⑵a⊥b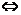 a·b=0
a·b=0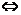
 .
.
4.
向量的直角坐标运算:设a= ,b=
,b= ,则
,则
⑴a+b=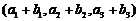 ; ⑵a-b=
; ⑵a-b=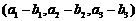 ;
;
⑶λa=
 ; ⑷a·b=
; ⑷a·b=
证明方法:与平面向量一样,将a=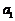 i+
i+ j+
j+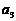 k和b
k和b =
=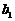 i+
i+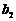 j+
j+ k代入即可.
k代入即可.
3.
空间向量的坐标表示:给定一个空间直角坐标系和向量a,且设i、j、k为坐标向量,则存在唯一的有序实数组 ,使a=
,使a=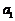 i+
i+ j+
j+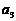 k.
k.
空间中相等的向量其坐标是相同的.→讨论:向量坐标与点的坐标的关系?
 向量在空间直角坐标系中的坐标的求法:设A
向量在空间直角坐标系中的坐标的求法:设A ,B
,B ,则
,则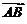 =
= -
- =
= -
- =
= .
.
2. 单位正交基底:如果空间一个基底的三个基向量互相垂直,且长度都为1,则这个基底叫做单位正交基底,通常用{i,j,k}表示.
单位--三个基向量的长度都为1;正交--三个基向量互相垂直.
 选取空间一点O和一个单位正交基底{i,j,k},以点O为原点,分别以i,j,k的方向为正方向建立三条坐标轴:x轴、y轴、z轴,得到空间直角坐标系O-xyz,
选取空间一点O和一个单位正交基底{i,j,k},以点O为原点,分别以i,j,k的方向为正方向建立三条坐标轴:x轴、y轴、z轴,得到空间直角坐标系O-xyz,
1. 类比:由平面向量的基本定理,对平面内的任意向量 ,均可分解为不共线的两个向量
,均可分解为不共线的两个向量 和
和 ,使
,使 . 如果
. 如果 时,这种分解就是平面向量的正交分解. 如果取
时,这种分解就是平面向量的正交分解. 如果取 为平面直角坐标系的坐标轴方向的两个单位向量
为平面直角坐标系的坐标轴方向的两个单位向量 ,则存在一对实数x、y,使得
,则存在一对实数x、y,使得 ,即得到平面向量的坐标表示
,即得到平面向量的坐标表示 .
.
推广到空间向量,结论会如何呢?
(1)空间向量的正交分解:对空间的任意向量 ,均可分解为不共面的三个向量
,均可分解为不共面的三个向量 、
、 、
、 ,使
,使 . 如果
. 如果 两两垂直,这种分解就是空间向量的正交分解.
两两垂直,这种分解就是空间向量的正交分解.
 (2)空间向量基本定理:如果三个向量
(2)空间向量基本定理:如果三个向量 不共面,那么对空间任一向量
不共面,那么对空间任一向量 ,存在有序实数组
,存在有序实数组 ,使得
,使得 . 把
. 把 叫做空间的一个
叫做空间的一个 基底(base),
基底(base), 都叫做基向量.
都叫做基向量.
1. 回顾:平面向量的加减与数乘运算以及平面向量的坐标运算,
作业:课本P101 例4
第五课时3.1.4空间向量的正交分解及其坐标表示
教学要求:掌握空间向量的正交分解及空间向量基本定理和坐标表示;掌握空间向量的坐标运算的规律;会根据向量的坐标,判断两个向量共线或垂直.
教学重点:空间向量基本定理、向量的坐标运算.
教学难点:理解空间向量基本定理.
教学过程:
5. 教学例题:课本P98例2、例3(略)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com