
作业:课本P105练习 3题.
5. 用向量方法证明:如果两条直线同垂直于一个 平面,则这两条直线平行.
平面,则这两条直线平行.
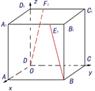
4. 出示例5:如图,在正方体 中,
中, ,求
,求 与
与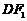 所成的角的余弦值.
所成的角的余弦值.
分析:如何建系? → 点的坐标? → 如何用向量运算求夹角? → 变式:课本P104、例6
3. 练习:已知A(3,3,1)、B(1,0,5),求:⑴线段AB的中点坐标和长度;⑵到A、B两点距离相等的点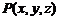 的坐标x、y、z满足的条件. (答案:(2,
的坐标x、y、z满足的条件. (答案:(2, ,3);
,3); ;
;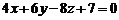 )
)
 说明:⑴中点坐标公式:
说明:⑴中点坐标公式: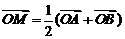 =
= ;
;
⑵中点p的轨迹是线段AB的垂直平分平面.在空间中,关于x、y、z的三元一次方程的图形是平面.
3. 两点间距离共识:利用向量的长度公式,我们还可以得出空间两点间的距离公式:
在空间直角坐标系中,已知点 ,
,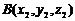 ,则
,则
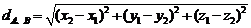 ,其中
,其中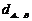 表示A与B两点间的距离.
表示A与B两点间的距离.
⒈
向量的模:设a= ,b=
,b= ,求这两个向量的模.
,求这两个向量的模.
|a|=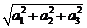 ,|b|=
,|b|= .这两个式子我们称为向量的长度公式.
.这两个式子我们称为向量的长度公式.
这个公式的几何意义是表示长方体的对角线的长度.
2. 夹角公式推导:∵ a·b=|a||b|cos<a,b>
∴  =
=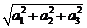 ·
· ·cos<a,b>
·cos<a,b>
由此可以得出:cos<a,b>=
这个公式成为两个向量的夹角公式.利用这个共识,我们可以求出两个向量的夹角,并可以进一步得出两个向量的某些特殊位置关系:
当cos<a、b>=1时,a与b同向;当cos<a、b>=-1时,a与b反向;
当cos<a、b>=0时,a⊥b.
2. 怎样求一个空间向量的坐标呢?(表示这个向量的有向线段的终点的坐标减去起点的坐标.)
1. 向量的直角坐标运算法则:设a= ,b=
,b= ,则
,则
⑴a+b=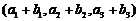 ; ⑵a-b=
; ⑵a-b=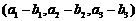 ;
;
⑶λa=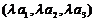
 ; ⑷a·b=
; ⑷a·b=
上述运算法则怎样证明呢?(将a=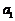 i+
i+ j+
j+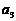 k和b=
k和b=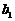 i+
i+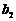 j+
j+ k代入即可)
k代入即可)
第六课时3.1.5空间向量运算的坐标表示(夹角和距离公式)
教学要求:掌握空间向量的长度公式、夹角公式、两点间距离公式、中点坐标公式,并会用这些公式解决有关问题.
教学重点:夹角公式、距离公式.
教学难点:夹角公式、距离公式的应用.
教学过程:
7. 出示例:课本P101 例4 . (解略)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com