
1. (2004年重庆卷)不等式 的解集是 (
)
的解集是 (
)
A. 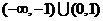 B.
B. 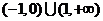
C. D.
D.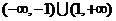
5.解含参数不等式,对所含字母分类讨论,必须不重不漏;
解含参数的二次不等式讨论的项目依次是(1)二次项系数,(2)有根无根,(3)根的大小.
4.指数不等式、对数不等式的解法:
(1)化同底,利用单调性,转化为代数不等式;注意对数式中的真数必大于零。
(2)换元法;整体代换,化繁为简。先解出新变量的解,再求原变量的解。
(3)非同底的指数式可两边取对数。
3.分式不等式的解法:
(1)解分式不等式一般化为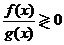 的形式;极特殊情况下,也可以同乘公分母,化整式,这时必须清楚所乘式子的符号。
的形式;极特殊情况下,也可以同乘公分母,化整式,这时必须清楚所乘式子的符号。
(2) 与f(x)·g(x)>0同解;
与f(x)·g(x)>0同解;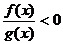 与f(x)·g(x)<0同解。转化为高次不等式求解,(若f(x),g(x)是整式)。
与f(x)·g(x)<0同解。转化为高次不等式求解,(若f(x),g(x)是整式)。
2.高次不等式的解法:分解因式,穿根法。
1.一元一次不等式(略),一元二次不等式,与二次函数、二次方程结合。
3.掌握解不等式的基本思路,即化归,分类、换元、数形结合等方法,通过解不等式的复习,提高分析问题、计算能力及解决问题的能力。
2.掌握指数、对数不等式的解法,会利用指数函数、对数函数的单调性,或用换元法解简单的指、对数不等式。
1.在熟练掌握一元一次不等式(组)、一元二次不等式的解法基础上,掌握简单分式不等式高次不等式的解法
3、所有答案都必须做在答题卷标定的位置上,务必注意试题序号和答题序号相对应
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com