
3.下列关于速度和加速度的说法中,正确的是( D )
A.物体运动的速度改变越大,它的加速度一定越大
B.物体运动的加速度为零,它的速度也一定为零
C.物体运动的速度改变越小,它的加速度一定越小
D.加速度的大小是表示物体运动速度随时间变化率的大小
2.物体的加速度为2m/s2,表示这物体 ( C )
A 每秒运动2m B每经过1秒,其速度增大2m/s2
C 每经过1秒,其速度增大2m/s D每经过1秒,其速度增大2m
1.下列关于加速度的说法中正确的是( B )
A.加速度表示物体运动的快慢 B.加速度表示物体速度变化的快慢
C.物体运动速度越大,其加速度越大 D.物体运动速度为零,其加速度一定也为零
4.在“速度-时间”图像中,加速度是图线的斜率。速度图线越陡,加速度越大;速度图线为水平线,加速度为0。
[范例精析]
例1试举出下列实例:(1)速度很大而加速度较小,甚至为0;(2)速度很小而加速度很大;(3)加速度为0而速度不为0;(4)速度为0而加速度不为0。 (5)速度方向与加速度方向相反。
解析:(1)高速飞行的飞机速度很大,但加速度不一定也很大,甚至可能为0(当飞机高速匀速飞行时);
(2)子弹在枪膛里刚被激发时,速度很小而加速度很大;
(3)一切匀速运动的物体加速度为0而速度不为0;
(4)刚启动时刻的汽车、火车,速度为0而加速度不为0,竖直向上抛出的石子在最高点时速度为0而加速度不为0。
(5)汽车刹车后停止运动前作减速运动过程中,速度方向与加速度方向相反。
拓展:由例1可知,速度和加速度是完全不同的物理量。大小不成比例,方向不一定相同。
例2.篮球以6m/s的速度竖直向下碰地面,然后以4m/s速度竖直向上反弹,碰地的时间为0.2秒。
(1)求篮球在这0.2秒内的速度变化Δv。
(2)有的同学这样计算球的加速度:a =(v2-v1)/ t=(4-6)/0.2m/s2=-10m/s2。他的方法对吗?为什么?正确的是多少?
解析:(1)Δv =v2- v1= -10m/s
(2)不对。他没有注意速度的方向。正确解法为:
以向下为正方向,v1=+6m/s,v2=-4m/s,加速度为
a =(v2-v1)/ t=(-4-6)/0.2m/s2=-50m/s2
负号表示加速度方向与正方向相反,即向上。
拓展:加速度的定义式为矢量式,只要规定正方向,速度和加速度均可以用带有正负号的代数量表示,在解题时要特别注意各个量正负号的确定。已知量代入公式时必须冠以符号,未知量一般可先假设为正,求解后再作出判断说明。
例3 .如图1-5-1所示,是一电梯由底楼上升到顶楼过程中速度随时间的变化图象,电梯的运动速度如何变化的?各段时间内电梯的加速度各是多大?
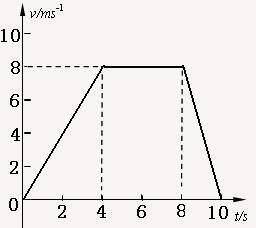
解析: 电梯从底楼到顶楼总的运动时间为10s,这10s可分为三个阶段:
第一阶段:0到4s末,速度由0增大到8m/s,是一个加速运动阶段。
第二阶段:从4s末到8s末,速度保持8m/s不变,是一个匀速运动阶段。
第三阶段:从8s末到10s末,速度由8m/s减小到0,是一个减速运动阶段。
由加速度的定义式a =Δv/Δt可求得:第一阶段的加速度a1=(8-0)/(8-4)m/s2=2m/s2,第二阶段的加速度a2=(8-8)/(8-4)m/s2=0,第三阶段的加速度a3=(0-8)/(10-8)m/s2=-4m/s2,-号表示电梯在做减速运动,表示加速度的方向与速度方向相反。
拓展:第三阶段的加速度与第一阶段的加速度哪个大呢?很多同学可能会说,当然是a1大了!因为a3是负的,a1是正的。但是这个看法却是错的。
加速度是矢量,要比较矢量的大小,只要看其绝对值的大小,负号只是表示其方向。所以是a3比a1(的绝对值)大。
[能力训练]
3.还有一个量也要注意与速度和加速度加以区分,那就是“速度变化量”Δv,Δv = v2 - v1。Δv越大,加速度并不一定越大,还要看所用的时间的多少。
2.加速度与速度是完全不同的物理量,加速度是速度的变化率。所以,两者之间并不存在“速度大加速度也大、速度为0时加速度也为0”等关系,加速度和速度的方向也没有必然相同的关系,加速直线运动的物体,加速度方向与速度方向相同;减速直线运动的物体,加速度方向与速度方向相反。
[要点导学]
1.加速度的物理意义:反映运动物体速度变化快慢的物理量。
加速度的定义:速度的变化与发生这一变化所用的时间的比值,即a =Δv/Δt=(v2-v1)/Δt。
加速度是矢量。加速度的方向与速度方向并不一定相同。
2.对于物体运动的情况,可以用列表法进行描述.下面表格中的数据就是某物体做直线运动过程中测得的位移x和时间t的数据记录,试根据表中的记录分析,并寻找s随t变化的规律.
|
物体运动起始点 |
所测物理量 |
测量次数 |
||||
|
l |
2 |
3 |
4 |
5 |
||
|
A→B |
时间t/s |
0.55 |
1.09 |
1.67 |
2.23 |
2.74 |
|
位移x/m |
0.2511 |
0.5052 |
0.7493 |
1.0014 |
1.2547 |
|
|
B→A |
时间t/s |
0.89 |
1.24 |
1.52 |
1.76 |
1.97 |
|
位移x/m |
0.2545 |
0.5009 |
0.7450 |
1.0036 |
1.2549 |
A到B时位移与时间成正比,B到A时位移与时间的平方成正比(提示:可用图象法寻找规律)
1.运动物体拉动穿过打点计时器的纸带,纸带上打下一系列小点.打点计时器打下的点直接记录了 ( AB )
A.物体运动的时间 B、物体在不同时刻的位置
C.物体在不同时刻的速度 D.物体在不同时间内的位移
5.以时间t为横坐标、瞬时速度v为纵坐标,画出的表示物体速度随时间变化关系的图线,称为速度-时间图线(v-t图线),简称速度图线(或速度图像)。
[范例精析]
例题 .图1-4-1是一位同学利用电磁打点计时器打出的一条纸带,相邻点的时间间隔为0.02s,纸带旁边是一支最小刻度为1mm的直尺,试计算拖着纸带做直线运动的物体在AC这段时间内的平均速度和在B点的瞬时速度。

解析: AC这段时间内的平均速度就等于A到C的位移跟所用的时间的比值。位移的大小从刻度尺上读出:x=4.20cm,A到C共11个点,10个时间间隔,所以A到C所用的时间t=0.02s×10=0.2s,所以
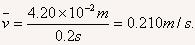
根据公式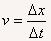 计算B点的瞬时速度,为了尽量精确地反映物体在B点的运动快慢,我们尽量在靠近B点的地方取得数据,例如取靠近B点的左右两个点子,左边一个点子在刻度尺上的读数是1.73cm,右边一个点子在刻度尺上的读数是2.61cm,那么Δx=2.61-1.73cm=0.88cm,两点间相隔的时间为Δt =0.02s×2= 0.04s,所以
计算B点的瞬时速度,为了尽量精确地反映物体在B点的运动快慢,我们尽量在靠近B点的地方取得数据,例如取靠近B点的左右两个点子,左边一个点子在刻度尺上的读数是1.73cm,右边一个点子在刻度尺上的读数是2.61cm,那么Δx=2.61-1.73cm=0.88cm,两点间相隔的时间为Δt =0.02s×2= 0.04s,所以
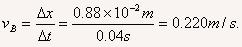
拓展: 用最小刻度是mm的尺,读数时应该估读到0.1mm位,不能为了“方便”而“凑整数”,这是实验的规则。
[能力训练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com