
2.汽车从静止开始以1m/s2的加速度运动,则汽车5s内通过的位移为________m,第2s内的平均速度为__________m/s,第2s内的位移是________m。1.5,1.5
1.⑴物体的初速度为2m/s,加速度为2m/s2,当它的速度增大到6m/s时,所通过的路程x= .8m
⑵某物体的初速度为2m/s,在4 s的时间内速度均匀增大到6m/s,那么该物体在这段时间内发生的位移x为 m.16
⑶飞机在跑道上滑行,离地起飞时的速度是60m/s,若飞行滑行时加速度大小为4m/s2,则飞机从开始滑行至起飞需时间 s,起飞的跑道长至少为 m.15,450
4.匀变速直线运动的平均速度
由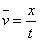 和
和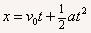 可得
可得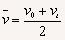 ,应用此式时请注意:
,应用此式时请注意:
(1)此式只适用于匀变速直线运动,不论是匀加速直线运动还是匀减速直线运动都适用,但对非匀变速直线运动的平均速度只能用平均速度的定义式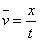 来计算。
来计算。
(2)式中的“v0+vt”是矢量和,不是代数和。对匀变速直线运动来说,v0和vt在一条直线上,可以通过规定正方向,把矢量运算转化为代数运算。
(3)由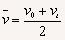 和速度公式vt=v0+at得
和速度公式vt=v0+at得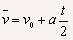 =vt/2,即时间t内的平均速度等于中间时刻的瞬时速度。
=vt/2,即时间t内的平均速度等于中间时刻的瞬时速度。
[范例精析]
例1:一物体做匀加速直线运动,初速度为v0=5m/s,加速度为a=0.5m/s2,求:
(1)物体在3s内的位移;
(2)物体在第3s内的位移。
解析:计算物体运动的位移,应该认清是哪一段时间内的位移,第一小题所求位移的时间间隔是3s,第二小题所求位移的时间间隔是1s,即2s末到3s末的位移;因为物体做匀加速直线运动,可以运用匀加速直线运动的公式来计算。
(1)用位移公式求解
3s内物体的位移:x3=v0t3+at32/2=5×3+0.5×32/2=17.25m
(2)由(1)知x3=17.25m,又
2s内物体的位移:x2=v0t2+at22/2=5×2+0.5×22/2=11m
因此,第3s内的位移:x=x3-x2=17.25-11=6.25(m)
用平均速度求解:
2s末的速度:v2=v0+at2=5+0.5×2=6m/s
3s末的速度:v3=v0+at3=5+0.5×3=6.5m/s
因此,第3s内的平均速度: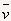 =(v2+v3)/2=6.25m/s
=(v2+v3)/2=6.25m/s
第3s内的位移:x=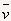 t=6.25×1=6.25(m)
t=6.25×1=6.25(m)
拓展:解题过程中,审题要仔细,并正确理解公式的含义,明辩各时间段的意义;运动学问题的求解方法一般不唯一,可适当增加一题多解的练习,培养思维的发散性,提高应用知识的灵活性。
例2: 一辆汽车刹车前速度为90km/h,刹车获得的加速度大小为10m/s2,求:
(1)汽车刹车开始后10s内滑行的距离x0;
(2)从开始刹车到汽车位移为30m时所经历的时间t;
(3)汽车静止前1s内滑行的距离x/;
解析:(1)判断汽车刹车所经历的时间
v0=90km/h=25m/s
由0=v0+at及a=-10m/s2得:t=-v0/a=25/10=2.5s<10s
汽车刹车后经过2.5s停下来,因此10s内汽车的位移只是2.5s内的位移。
解法一:利用位移公式求解
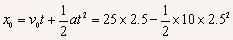 =31.25m
=31.25m
解法二:根据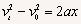 得:
得:
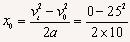 =31.25m
=31.25m
(2)根据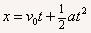 得:
得: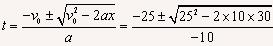
解得:t1=2s,t2=3s
t2是汽车经t1后继续前进到达最远点后,再反向加速运动重新到达位移是30m处时所经历的时间,由于汽车刹车是单向运动,很显然,t2不合题意,须舍去。
(3)解法一:把汽车减速到速度为零的过程,看作初速为零的匀加速度运动过程,求出汽车以 10m/s2的加速度经过1s的位移,即: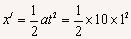 =5m
=5m
解法二:静止前1s末即是开始减速后的1.5s末,1.5s末的速度v1.5=v0+at=25-10×1.5=10(m/s)
所以: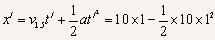 =5m
=5m
拓展:汽车刹车是单向运动,其速度减小到零就停止运动,分析运动过程要分清楚各阶段的运动性质,即汽车在减速,还是已经停止。将汽车减速到零的运动可以看成是初速为零的匀加速运动,可以使问题的解答更简捷。
例3:矿井里的升降机从静止开始做匀加速直线运动,上升3s后速度达到3m/s,然后匀速上升6s,最后匀减速上升2s停下,求升降机上升的高度,并画出升降机运动过程中的速度-时间图象。
解析:升降机的运动过程分为三个阶段:加速上升
阶段、匀速上升阶段和减速上升阶段。
在加速上升阶段,a1=(v-v0)/t1=1m/s2,
x1=a1t12/2=4.5m;
匀速上升阶段,x2=vt2=18m;
减速上升阶段,a3=(vt-v)/t3=-1.5m/s2
x3=vt3+a1t32/2=3m;
所以,升降机上升高度x=x1+x2+x3=25.5m,其运动过程的v-t图象如图2-3-3所示。
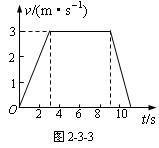
拓展:本题除上述解法外,还可利用平均速度定义式和条件式组合解题,升降机运动过程的第一、第三阶段的平均速度都是1.5m/s,这两过程中上升的高度一共为1.5×5m=7.5m。还可利用v-t图象解题,升降机上升的总高度即v-t图象中图线所包围的面积,同学们自己可以试一试。
[能力训练]
3.匀变速直线运动速度与位移的关系
由速度公式vt=v0+at和位移公式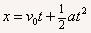 联立消去时间t,可得速度与位移的关系式:vt2-v02=2ax
联立消去时间t,可得速度与位移的关系式:vt2-v02=2ax
此式是匀变速直线运动规律的一个重要推论,如果问题的已知量和未知量都不涉及时间,应用此式求解比较方便,对于初速度为零的匀变速直线运动,此式可简化为_______。
2.对匀变速直线运动位移公式: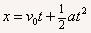 的理解
的理解
(1)式中共有四个物理量,仅就该公式而言,知三求一;
(2)式中x、v0、a是矢量,在取初速度v0方向为正方向的前提下,匀加速直线运动a取正值,匀减速直线运动a取______,计算的结果x>0,说明位移的方向与初速度方向______,x<0,说明位移的方向与初速度方向________。
(3)对于初速度为零的匀加速直线运动,位移公式为:x=at2/2
[要点导学]
1.位移公式
物体做匀速直线运动的v-t图线如图2-3-1所示,在时间t内物体的位移对应v-t图象中矩形OCAB的面积,对应匀速直线运动物体的位移公式:x=vt;物体做匀变速直线运动的v-t,图线如图2-3-2所示,同理可知,在时间t内物体的位移对应v-t图象中梯形ODEF的面积,因此,匀变速度直线运动物体的位移公式为_____________________。
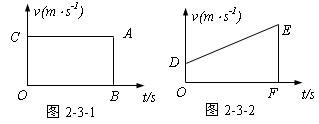
此位移公式是采用“微元法”把匀变速直线运动转化为匀速直线运动推导出来的,同学们应结合教材内容,深入理解这一研究方法及位移公式的推导过程,并加以应用。
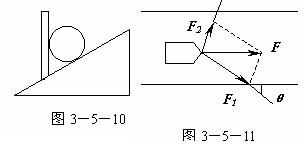
11.如图3-5-11所示,一个大人沿与河岸成θ角的方向拉纤,要使平行河岸的船行方向上得到一个合力F,则另一岸的一个小孩如何用力最小.与F垂直 F1sinθ
10.如图3-5-10所示,一光滑小球静止于斜面与竖直挡板之间,已知小球受到的重力为100N。试回答下列几个问题:
(1).光滑小球受到哪几个力的作用,画出受力图。
(2).用作图法求出球所受重力沿水平方向和垂直斜面方向的两个分力。
(3).以上两个分力与球对竖直挡板、对斜面的压力有怎样的关系?相等
9、把一个向东的大小为60N的力分解为两个分力,其中一个分力向南并等于80N,用作图法求出另一个分力。F2=100N,方向东偏北53°
8.图3-5-9的各图所示的重物A静止。试根据力的效果把A的重力分解,并把重力的分解示意图画在对应的图上。

答案: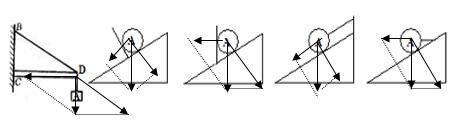
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com