9．竖直放置两端封闭的玻璃管内注满清水和一个用红蜡做成的圆柱体，玻璃管倒置时圆柱体能匀速上浮，现将玻璃管倒置，在圆柱体匀速上浮的同时，使玻璃管水平匀速运动，已知圆柱体运动的速度是0.05m/s，θ＝60⁰，如图所示，则玻璃水平运动的速度是多大？ 0.025m/s

8．河宽300m，水流速度为3m/s，小船在静水中的速度为5m/s，问

(1)以最短时间渡河，时间为多少?可达对岸的什么位置?

(2)以最短航程渡河，船头应向何处?渡河时间又为多少?

(1)当船头对准对岸行驶时(并不是到达正对岸)，时间最短，最短时间60s，到达对岸，在出发点下游180m (2)由于v₁＞v₂，所以船可以垂直到正对岸，船头与河岸上游夹角为α＝arccos(3/5)，渡河时间75s

7．如图所示，某船在河中向东匀速直线航行，船上的人正相对于船以0.4m/s的速度匀速地竖直向上升起一面旗帜，当他用20s升旗完毕时，船行驶了9m，那么旗相对于岸的速度大小是多少? 0.6m/s

6．两个相互垂直的运动，一个是匀速，另一个是初速度为零的匀加速运动，其合运动一定是________(填“直线运动”或“曲线运动”)曲线运动

5．一人站在匀速运动的自动扶梯上，经时间20s到楼上，若自动扶梯不动，人沿扶梯匀速上楼需要时间30s，当自动扶梯匀速运动的同时，人沿扶梯匀速(相对扶梯的速度不变)上楼，则人到达楼上所需的时间为________s 12

4．一个物体的运动由水平的匀加速度a₁=4m/s²和竖直的匀加速度a₂=3m/s²两个分运动组成，关于这个物体的运动加速度说法正确的是( B )

A．加速度的数值在1－7m/s²之间　　　　　 B．加速度的值为5m/s²

C．加速度数值为7m/s²　　　　　　　　　　 D．加速度数值为lm/s²

3．一船以恒定的速率渡河，水流速度恒定(小于船速)，要使船垂直到达对岸，则(　 B　 )

　 A．船应垂直河岸航行　

　 B．船的航行方向应偏向上游一侧

　 C．船不可能沿直线到达对岸

D．河的宽度一定时，船到对岸的时间是任意的

2．如果两个不在同一直线上的分运动都是匀速直线运动，对其合运动的描述中，正确的是 ( B )

　 A．合运动一定是曲线运动

　 B．合运动一定是直线运动　 　

　 C．合运动是曲线运动或直线运动

D．当两个分运动的速度数值相等时，合运动才为直线运动

1．一人游泳渡河以垂直河岸不变的速度(相对水)向对岸游去，河水流动速度恒定．下列说法中正确的是 ( D )

　 A．河水流动速度对人渡河无任何影响

　 B．游泳渡河的路线与河岸垂直

　 C．由于河水流动的影响，人到达对岸的时间与静水中不同

D．由于河水流动的影响，人到达对岸的位置，向下游方向偏移

5．决定合运动的性质和轨迹的因素

物体运动的性质由加速度决定(加速度为零时物体静止或做匀速运动；加速度恒定时物体做匀变速运动；加速度变化时物体做变加速运动)。

物体运动的轨迹(直线还是曲线)则由物体的速度和加速度的方向关系决定(速度与加速度方向在同一条直线上时物体做直线运动；速度和加速度方向成角度时物体做曲线运动)。

两个互成角度的直线运动的合运动是直线运动还是曲线运动？

决定于它们的合速度和合加速度方向是否共线(如图1所示)。　

常见的类型有：

(1)a=0：匀速直线运动或静止。

(2)a恒定：性质为匀变速运动，分为：① v、a同向，匀加速直线运动；②v、a反向，匀减速直线运动；③v、a成角度，匀变速曲线运动(轨迹在v、a之间，和速度v的方向相切，方向逐渐向a的方向接近，但不可能达到。)

(3)a变化：性质为变加速运动，加速度大小、方向都随时间变化。

[范例精析]

例1．无风时气球匀速竖直上升的速度是4m/s，现自西向东的风速大小为3m/s，则

(1)气球相对地面运动的速度大小为　　　，方向　　　。

(2)若风速增大，则气球在某一时间内上升的高度与风速增大前相比将　　。(填“增大”、“减小”、“保持不变”)

解析：(1)题中气球的运动，在地面上的人看来，它同时参与了两个运动，即竖直向上的运动和自西向东的水平运动，其合速度与其关系为：

v²＝v_竖²+v_东²

设合速度方向与水平方向夹角为θ，则：

tanθ＝v_竖/v_东

代入数据可得：合速度大小v＝5m/s，θ＝arctan1.33＝53°，即合速度的方向为向东偏上53°。

(2)如果一个物体同时参与两个运动，这两个分运动是“相互独立、同时进行”的，各自遵守各自的规律。本题中，由风引起的水平方向的分运动不会影响气球竖直方向的分运动，所以不管水平方向的风速如何变化，气球在同一时间内上升的高度总是一定的。

拓展：从本例不难看出，要正确解答有关运动的合成与分解的问题，首先要认清合运动和分运动，实际发生的运动就是合运动，参与而实际并没发生的运动就是分运动；二要正确理解运动的独立性原理；三要掌握运动的合成与分解的法则，灵活运用平行四边形定则。

例2.河宽d=100m，水流速度为v₁=4m/s，船在静水中的速度是v₂=3m/s，求：

(1)欲使船渡河时间最短，船应怎样渡河？最短时间是多少？船经过的位移是多大？

(2)欲使船航行距离最短，船应怎样渡河？渡河时间多长？

解析： 设想水不流动，则船将以v₁速度做匀速直线运动，设想船不开行，则船将以v₂速度顺水飘流，可见实际渡河时，渡船同时参与两个分运动，其合运动沿v₁与v₂矢量和的方向做匀速直线运动，由于分运动与合运动的等时性，船渡河时间等于v₁分运动的时间。

(1)不论v₁与v₂的大小如何，船头v₁的方向垂直指向河岸时，时间最短，t=x₁/v₁=d/v₁=(100/4)s=25s

(2)因船速小于水速，故小船不能垂直过河，但有无最短航程呢？

虽然不能垂直过河，但有最短的路程，用画圆的方法可找出最短船程时夹角θ，并可找到这时速度之间关系满足的特征，如图。

则sinθ=v₁/v₂

x=d/sinθ ，t=s/v_合=d/(sinθ)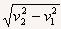

拓展：(1)不论v₁与v₂的大小如何，当船头v₁的方向垂直指向河岸时，时间最短，且最短时间为 。

(2) 当v₁＞v₂时，合速度垂直过岸，航程最短为d，当v₁＜v₂时不能垂直过岸，但仍有最短路程，此时船的实际航向与下游夹θ角，且sinθ=v₁/v₂。

[能力训练]