
[要点导学]
1.牛顿经过长期的研究思考,提出了他的假想:行星与太阳间的引力、地球吸引月球的力以及地球表面物体所受到的引力都是同一种性质的力,遵循同一个规律,即它们的大小都与距离的二次方成反比。
8.如果牛顿推导的太阳与行星间引力的表达式中,引力的大小与其距离的n次方(n≠2)成反比,各行星的周期与其轨道半径的二次方成正比,则n的值是多大?n=3
7.假设某星球的质量约为地球质量的9倍,半径约为地球的一半。若地球上近地卫星的周期为84分钟.则该星球上的近地卫星的周期是多少?9.9分钟
6.假设地球与月球间的引力与地球表面物体受到的重力是同种性质的力,即力的大小与距离的二次方成反比。已知月心和地心的距离是地球半径的60倍,地球表面的重力加速度为9.8m/s2,试计算月球绕地球做圆周运动的向心加速度。3×10-3m/s2
5.若火星和地球都绕太阳做匀速圆周运动,今知道地球的质量、公转的周期和地球与太阳之间的距离,今又测得火星绕太阳运动的周期,则由上述已知量可求出(BCD)
A.火星的质量
B.火星与太阳间的距离
C.火星的加速度大小
D.火星做匀速圆周运动的速度大小
4.在宇宙发展演化的理论中,有一种学说叫“宇宙膨胀说”,就是天体的距离在不断增大,根据这理论,在很久很久以前,太阳系中地球的公转情况与现在相比(BC)
A.公转半径较大
B.公转周期较小
C.公转速率较大
D.公转角速度较小
3.关于太阳与行星间的引力,下列说法正确的是(BCD)
A.神圣和永恒的天体的匀速圆周运动无需要原因,因为圆周运动是最美的。
B.行星绕太阳旋转的向心力来自太阳对行星的引力
C.牛顿认为物体运动状态发生改变的原因是受到力的作用。行星围绕太阳运动,一定受到了力的作用。
D.牛顿把地面上的动力学关系应用到天体间的相互作用,推导出了太阳与行星间的引力关系
2.对于太阳与行星间引力的表述式 ,下面说法中正确的是(D)
,下面说法中正确的是(D)
A.公式中G为引力常量,它是人为规定的
B.当r趋近于零时,太阳与行星间的引力趋于无穷大
C.太阳与行星受到的引力总是大小相等的、方向相反,是一对平衡力
D.太阳与行星受到的引力总是大小相等的、方向相反,是一对作用力与反作用力
1.有一星球的密度与地球的密度相同,但它表面处的重力加速度是地面上重力加速度的4倍,则该星球的质量将是地球质量的(D )
A. 1/4 B. 4倍 C. 16倍 D. 64倍。
2.太阳与行星间的引力推导思路(将椭圆轨道近似看作圆轨道来推导):
(1)行星运动需要的向心力: ,根据开普勒第三定律:
,根据开普勒第三定律: 得到:太阳对行星的引力
得到:太阳对行星的引力 (其中m为行星质量,r为行星与太阳的距离)
(其中m为行星质量,r为行星与太阳的距离)
(2)太阳和行星在相互作用中的地位是相同的,只要作相应的代换,就可以得到结果。行星对太阳的引力 (其中M为太阳的质量,r为太阳到行星的距离)
(其中M为太阳的质量,r为太阳到行星的距离)
(3)因为这两个力是作用力与反作用力,大小相等,所以概括起来,得到 ,写成等式,比例系数用G表示,有
,写成等式,比例系数用G表示,有 。
。
(4)虽然在中学阶段只能将椭圆轨道近似看作圆轨道来推导,但仍要明确:牛顿是在椭圆轨道下进行推导的。牛顿是在前人的基础上做出了伟大发现,牛顿的发现还在于他有正确的科学思想和超凡的数学能力。
[范例精析]
例题:证明开普勒第三定律中,各行星绕太阳公转周期的平方与公转轨道半径的三次方的比值k是与太阳质量有关的恒量。
解析:行星绕太阳运动的原因是受到太阳的引力,引力的大小与行星质量、太阳质量及行星到太阳的距离(行星公转轨道半径)有关。这个引力使行星产生向心加速度,而向心加速度与行星公转的周期和轨道半径有关,这样就能建立太阳质量与行星公转周期和轨道半径之间的联系。
设太阳质量为M,某行星质量为m,行星绕太阳公转周期为T,半径为R。将行星轨道近似看作圆,万有引力提供行星公转的向心力,有
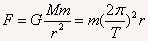
得到 ,
,
其中G是行星与太阳间引力公式中的比例系数,与太阳、行星都没有关系。可见星绕太阳公转周期的平方与公转轨道半径的三次方的比值k是与太阳质量有关的恒量。
拓展:在解决有关行星运动问题时,常常用到这样的思路:将行星的运动近似看作匀速圆周运动,而匀速圆周运动的向心力则由太阳对行星的引力提供。研究其它天体运动也同样可以用这个思路,只是天体运动的向心力由处在圆心处的天体对它的引力提供。
[能力训练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com