
2.经典力学的局限
和任何理论一样,经典力学也有它的局限性,有它的适用范围。
(1)从低速到高速--狭义相对论:当物体运动的速度比真空中的光速小得多时,质量、时间和长度的变化很小,可以忽略,经典力学完全适用。但如果物体运动速度可以和光速相比较时,质量、时间和长度的变化就很大,经典力学就不再适用,狭义相对论阐述了物体在以接近光速运动时所遵循的规律。
(2)从宏观到微观--量子力学:物理学研究深入到微观世界,发现微观粒子不但具有粒子的性质,还能产生干涉、衍射现象。干涉和衍射是波所特有的性质。也就是说微观粒子具有波动性。这是牛顿经典力学无法解释的。正是在这种情形下,量子力学应运而生,量子力学能够很好地解释微观粒子的运动规律。
(3)从弱引力到强引力--广义相对论:天文观测发现行星的轨道并不严格闭合,它们的近日点在不断地旋进。这种现象称为行星的轨道旋进。这是用牛顿万有引力定律无法得到满意解释的。爱因斯坦创立了广义相对论,根据广义相对论计算出的水星近日点的旋进与天文观测能很好地吻合,爱因斯坦创立的广义相对论是一种新的时空引力理论,爱因斯坦还根据广义相对论预言了光线在经过大质量星体附近时会发生偏转,这也是被天文观测所证实的。
根据牛顿万有引力定律,假定一个球形天体总质量不变,并通过压缩减小它的半径,天体表面上的引力将会增加。半径减小到原来的二分之一,引力增大到原来的四倍。爱因斯坦引力理论表明,这个力实际上增大得更快些。天体半径越小,这种差别越大。根据牛顿的理论,当天体被压缩成半径几乎为零的一个点时,引力趋于无穷大。爱因斯坦的理论则不然,引力趋于无穷大发生在半径接近一个“引力半径”的时候。这个引力半径的值由天体的质量决定,例如太阳的引力半径为3km,地球的引力半径为1m。因此,只要天体的实际半径远大于它们的引力半径,那么由爱因斯坦和牛顿引力理论计算出的力的差异并不大。但当天体的实际半径接近引力半径时,这种差异将急剧增大。这就是说,在强引力的情况下,牛顿引力理论将不再适用。
[要点导学]
1.以牛顿运动定律为基础的经典力学,在万有引力定律建立后,更趋完美。几乎能解释当时所能看到的从天体到地面上的物体的运动现象,而且是那么地与实际相符合。于是经典力学就被人们广泛接受,并被用到实际中去,带来了许多新技术革命,对人们的生产和生活带来了重大的影响。
12.1997年8月26日在日本举行的国际学术大会上,德国Max Plank学会的一个研究组宣布了他们的研究结果:银河系的中心可能存在一个大“黑洞”。所谓“黑洞”,它是某些天体的最后演变结果。
(1)根据长期观测发现,距离某“黑洞”6.0×1012m的另一个星体(设其质量为m2)以2×106m/s的速度绕“黑洞”旋转,求该“黑洞”的质量m1;(结果要求二位有效数字)
(2)根据天体物理学知识,物体从某天体上的逃逸速度公式为v=  ,其中引力常量G=6.67×10-11Nm2/kg-2,M为天体质量,R为天体半径。且已知逃逸的速度大于真空中光速的天体叫“黑洞”。请估算(1)中“黑洞”的可能最大半径。(结果要求一位有效数字)
,其中引力常量G=6.67×10-11Nm2/kg-2,M为天体质量,R为天体半径。且已知逃逸的速度大于真空中光速的天体叫“黑洞”。请估算(1)中“黑洞”的可能最大半径。(结果要求一位有效数字)
11.组成星球的物质是靠引力吸引在一起的,这样的星球有一个最大的自转速率,如果超过了该速率,星球的万有引力将不足以维持赤道附近的物体做圆周运动。已知一个星球的质量为M,半径为R,假设该星球是均匀分布的,求它的最小自转周期。

7.宇航员在一个半径为R的星球上,以速度v0竖直上抛一个物体,经过t秒后物体落回原抛物点,如果宇航员想把这个物体沿星球表面水平抛,而使它不再落回星球,则抛出速度至少应是(B)

3.地球半径为R,地面重力加速度为g,地球自转周期为T,地球同步卫星离地面的高度为h,则地球同步卫星的线速度大小为(AC)
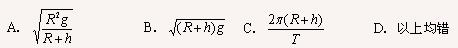
7.如果星球的密度很大,它的质量很大而半径又很小,它表面的逃逸速度很大,连光都不能逃逸,那么即使它确实在发光,光也不能进入太空,我们就看不到它。这种天体称为黑洞。
[范例精析]
例1:无人飞船“神舟二号”曾在离地面高度H=3.4×105m的圆轨道上运行了47h,求这段时间里它绕地球多少周?(地球半径R=6.37×106m,重力加速度g=9.8m/s2)
解析:47h内“神舟二号”绕地球运行多少周,也就是说47h有几个周期,本题关键是求“神舟二号”的运行周期。可以根据万有引力提供向心力这个思路来求周期T。
设“神舟二号”的质量为m,它在地面上的重力近似等于它受地球的万有引力,有
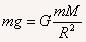
在空中运行时有
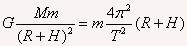
解得: =5474s=1.52h
=5474s=1.52h
47h内绕地球运行的圈数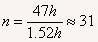 周
周
答:47h内“神舟二号”绕地球运行的圈数为31周。
拓展:本题主要综合应用万有引力定律,牛顿第二定律,和向心力公式,求圆周运动周期。其中又将物体在地球表面的重力近似看作物体受到的万有引力,由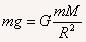 得到代换式:
得到代换式: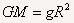 。向心加速度的表达式
。向心加速度的表达式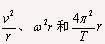 可根据具体问题选用。
可根据具体问题选用。
例2:已知地球半径R=6.4×106m,地球质量M=6.0×1024kg,地面附近的重力加速度g=9.8m/s2,第一宇宙速度v1=7.9×103m/s。若发射一颗地球同步卫星,使它在赤道上空运转,其高度和速度应为多大?
解析:所谓同步,就是卫星相对于地面静止即卫星运转周期等于地球自转周期。由于是万有引力提供向心力,卫星的轨道圆心应该在地球的地心,所以同步卫星的轨道只能在地球赤道上方。该题的计算思路仍然是万有引力提供向心力
设同步卫星的质量m,离地高度h,速度为v,周期为T(等于地球自转周期)
方法一: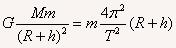
解得: =3.56×107m
=3.56×107m
 3.1×103m/s
3.1×103m/s
方法二:若认为同步卫星在地面上的重力等于地球的万有引力,有
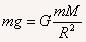
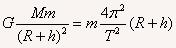
解联立方程得: =3.56×107m
=3.56×107m
方法三:根据第一宇宙速度v1,有
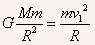
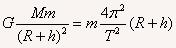
解得: =3.56×107m
=3.56×107m
答:同步卫星的高度为3.56×107m,速度是3.1×103m/s。
拓展:根据万有引力提供向心力列式求解,是解决此类问题的基本思路。在本题中又可以用地面重力加速度、第一宇宙速度这些已知量做相应代换。
本题计算得到的同步卫星运行速度为3.1×103m/s,比第一宇宙速度v1=7.9×103m/s小得多。第一宇宙速度是近地卫星的环绕速度,同步卫星是在高空中做匀速圆周运动,它的速度小于第一宇宙速度。同步卫星发射时的速度大于第一宇宙速度,一开始做大椭圆轨道运动,随后在高空中进行调整最后进入同步轨道做匀速圆周运动,速度比第一宇宙速度小。
[能力训练]
3.人造地球卫星
(1)人造地球卫星的轨道和运行速度
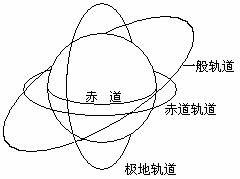
卫星地球做匀速圆周运动时,是地球的引力提供向心力,卫星受到地球的引力方向指向地心,而做圆周运动的向心力方向始终指向圆心,所以卫星圆周运动的圆心和地球的地心重合。这样就存在三类人造地球卫星轨道:①赤道轨道,卫星轨道在赤道平面,卫星始终处于赤道上方;②极地轨道,卫星轨道平面与赤道平面垂直,卫星通过两极上空;③一般轨道,卫星轨道和赤道成一定角度。
对于卫星的速度要区分发射速度和运行速度,发射速度是指将卫星发射到空中的过程中,在地面上卫星必需获得的速度,等于第一宇宙速度,卫星能在地面附近绕地球做匀速圆周运动,大于第一宇宙速度而小于第二宇宙速度时,卫星做以地球为焦点的椭圆轨道运动。运行速度是指卫星在正常轨道上运动时的速度,如果卫星做圆周运动,根据万有引力提供向心力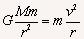 ,得
,得 ,可见,轨道半径越大,卫星的运行速度越小。实际上卫星从发射到正常运行中间经历了一个调整、变轨的复杂过程。
,可见,轨道半径越大,卫星的运行速度越小。实际上卫星从发射到正常运行中间经历了一个调整、变轨的复杂过程。
[要点导学]
1.第一宇宙速度的推导
方法一:设地球质量为M,半径为R,绕地球做匀速圆周运动的飞行器的质量为m,飞行器的速度(第一宇宙速度)为v。
飞行器运动所需的向心力是由万有引力提供的,近地卫星在“地面附近”飞行,可以用地球半径R代表卫星到地心的距离,所以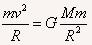 ,由此解出v=_____。
,由此解出v=_____。
方法二:物体在地球表面受到的引力可以近似认为等于重力,所以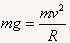 ,解得v=_____。
,解得v=_____。
关于第一宇宙速度有三种说法:第一宇宙速度是发射人造地球卫星所必须达到的最小速度,是近地卫星的环绕速度,是地球卫星的最大运行速度。
另外第一宇宙速度是卫星相对于地心的线速度。地面上发射卫星时的发射速度,是卫星获得的相对地面的速度与地球自转速度的合速度。所以赤道上自西向东发射卫星可以节省一定的能量。
3.6×1035kg 5×108m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com