
(二)过程:
 (一)细胞融合的生物学原理:细胞膜的流动性。
(一)细胞融合的生物学原理:细胞膜的流动性。
(二)应用
1、作物新品种的培育
(1)培育抗逆、高产及优质的转基因植株。
(2)单倍体育种和突变体的利用。
2、为遗传学、植物生理学和细胞生物学问题提供了良好的研究系统。
3、细胞产物的工业化生产:一些重要的细胞次生代谢产物(如某些中药)。
(一)过程(如右图)。
(二)植物组织培养过程
1、原理:细胞的全能性。
2、过程:(如图所示)。
3、注意事项
(1)取材:选取有形成层的部位最容易诱导形成愈伤组织。
(2)光照:在愈伤组织的诱导阶段往往要暗培养,有利于细胞脱分化产生愈伤组织。当愈伤组织分化出芽和叶时,一定要有光照,有利于叶片内叶绿素的合成。
4、细胞全能性表达的条件
(1)离体、无菌;
(2)一定的营养物质:水、无机盐、蔗糖、维生素等;
(3)激素:主要是细胞分裂素和生长素;
(4)适宜的温度和光照(培养后期)。
(5)全能性大小比较:受精卵>生殖细胞>体细胞;植物细胞>动物细胞。
 (一)植物细胞全能性:植物体的每个活细胞都具有遗传上的全能性,因而都具有发育为完整植株的潜能。
(一)植物细胞全能性:植物体的每个活细胞都具有遗传上的全能性,因而都具有发育为完整植株的潜能。
(二)克隆的条件
1、具有包含物种完整基因组的细胞核的活细胞。
2、能有效调控细胞核发育的细胞质物质。
3、完成胚胎发育的必要的环境条件。
(一)克隆技术的含义:用于分子、细胞水平的描述,指从众多的基因或细胞群体中通过无性繁殖和选择获得目的基因或特定类型细胞的技术操作。当用于个体水平描述时,克隆就是一种通过单个细胞,特别是来自特定个体的单个体细胞进行无性繁殖,从而产生新个体的过程或技术。
21.解:(1)设x<0,则-x>0
∵ 为偶函数, ∴
为偶函数, ∴
(2)∵ 为偶函数,∴
为偶函数,∴ =0的根关于0对称.
=0的根关于0对称.
由 =0恰有5个不同的实数解,知5个实根中有两个正根,二个负根,一个零根.
=0恰有5个不同的实数解,知5个实根中有两个正根,二个负根,一个零根.
且两个正根和二个负根互为相反数
∴原命题 图像与x轴恰有两个不同的交点
图像与x轴恰有两个不同的交点
下面研究x>0时的情况
∵
即  为单调增函数,故
为单调增函数,故 不可能有两实根
不可能有两实根
∴a>0 令
当 递减,
递减,
∴ 处取到极大值
处取到极大值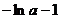
又当
要使 轴有两个交点当且仅当
轴有两个交点当且仅当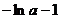 >0
>0
解得 ,故实数a的取值范围(0,
,故实数a的取值范围(0, )
)
方法二:
(2)∵ 为偶函数, ∴
为偶函数, ∴ =0的根关于0对称.
=0的根关于0对称.
由 =0恰有5个不同的实数解知5个实根中有两个正根,二个负根,一个零根.
=0恰有5个不同的实数解知5个实根中有两个正根,二个负根,一个零根.
且两个正根和二个负根互为相反数
∴原命题 图像与x轴恰有两个不同的交点
图像与x轴恰有两个不同的交点
下面研究x>0时的情况
 与直线
与直线 交点的个数.
交点的个数.
∴当 时,
时, 递增与直线y=ax下降或是x国,
递增与直线y=ax下降或是x国,
故交点的个数为1,不合题意 ∴a>0
 由几何意义知
由几何意义知 与直线y=ax交点的个数为2时,直线y=ax的变化应是从x轴到与
与直线y=ax交点的个数为2时,直线y=ax的变化应是从x轴到与 相切之间的情形.
相切之间的情形.
设切点
∴切线方为 
由切线与y=ax重合知
故实数a的取值范围为(0, )
)
17. 解:(1) 设 ,则
,则 …………………1分
…………………1分
 …………………2分
…………………2分
又 是奇函数,所以
是奇函数,所以 …………………3分
…………………3分

 =
= ……4分
……4分
………………5分
 是[-1,1]上增函数………………6分
是[-1,1]上增函数………………6分
(2)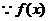 是[-1,1]上增函数,由已知得:
是[-1,1]上增函数,由已知得: …………7分
…………7分
等价于 …………10分
…………10分
解得: ,所以
,所以 …………12分
…………12分

 二次函数
二次函数 在
在 上递减………………………12分
上递减………………………12分
故 时,
时,
 ……………………13分
……………………13分
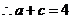 ,
, …………………………14分
…………………………14分
20 解:(1) ………………………………1分
………………………………1分

令 得
得 ………………………2分
………………………2分
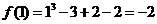
 拐点
拐点 ……………………………………3分
……………………………………3分
(2)设 是
是 图象上任意一点,则
图象上任意一点,则 ,因为
,因为 关于
关于 的对称点为
的对称点为 ,把
,把 代入
代入 得左边
得左边

右边

 右边=右边
右边=右边
 在
在 图象上
图象上

 关于A对称………………………………………7分
关于A对称………………………………………7分
结论:①任何三次函数的拐点,都是它的对称中心
②任何三次函数都有“拐点”
③任何三次函数都有“对称中心”(写出其中之一)……9分
(3)设 ,则
,则 ………………………10分
………………………10分
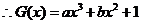 ,
, ,
,
 ,
, ,
, …………………11分
…………………11分
法一:





 ……………………………………13分
……………………………………13分
当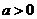 时,
时,
当 时,
时, 。。。。。。。14分
。。。。。。。14分
法二:  ,当
,当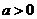 时,且
时,且 时,
时, ,
, 在
在 为凹函数,
为凹函数, ……………………………………13分
……………………………………13分
当 时,
时, ,
, 在
在 为凸函数
为凸函数
 …………………………………………14分
…………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com