
20.(14分)如图9-36,正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(Ⅰ)证明:AD⊥D1F; (Ⅱ)求AE与D1F所成的角;
(Ⅲ)证明:面AED⊥面A1FD1; (Ⅳ)设AA1=2,求三棱锥F-A1ED1的体积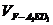 .
.
19.(14分)设{an}是正数组成的数列,其前n项和为Sn,并且对所有自然数n,an与2的等差中项等于Sn与2的等比中项.
(Ⅰ)写出数列{an}的前三项;
(Ⅱ)求数列{an}的通项公式(写出推证过程);
(Ⅲ)令bn=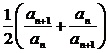 (n∈N*),求
(n∈N*),求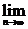 (b1+b2+…+bn-n).
(b1+b2+…+bn-n).
18. (12分)已知a>0,函数f(x)=ax-bx2.
(1)当b>0时,若对任意x∈R都有f(x)≤1,证明a≤2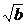 ;
;
(2)当b>1时,证明:对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤2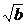 ;
;
(3)当0<b≤1时,讨论:对任意x∈[0,1],|f(x)|≤1的充要条件.
17. (8分) 一个电路中有三个电子元件,它们接通的概率都是m(0<m<1
(8分) 一个电路中有三个电子元件,它们接通的概率都是m(0<m<1 如图,有如下三种联接方法:
如图,有如下三种联接方法:
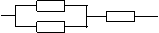
 ①
②
③
①
②
③
(1)分别求出这三种电路各自接通的概率;
(2)试分析这三种电路哪种性能最优,并证明你的结论.
16.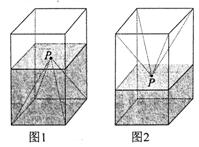 如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有
如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有 升水时,水面恰好经过正四棱锥的顶点
升水时,水面恰好经过正四棱锥的顶点 .如果将容器倒置,水面也恰好过点
.如果将容器倒置,水面也恰好过点 (图2).有下列四个命题:
(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半
B.将容器侧面水平放置时,水面也恰好过点
 C.任意摆放该容器,当水面静止时,水面都恰好
C.任意摆放该容器,当水面静止时,水面都恰好
经过点
D.若往容器内再注入 升水,则容器恰好能装满
升水,则容器恰好能装满
其中真命题的代号是 .(写出所有
真命题的代号) .
15.已知正四棱柱的对角线的长为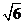 ,且对角线与底面所成角的余弦值为
,且对角线与底面所成角的余弦值为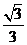 ,则该正四棱柱的体积等于
.
,则该正四棱柱的体积等于
.
14. 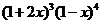 展开式中
展开式中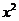 的系数为
.
的系数为
.
13.由1,2,3,4,5,6六个数可组成多少个无重复且是6的倍数的五位数是 .
12.有红、黄、蓝三种颜色的旗帜各3面,在每种颜色的3面旗帜上分别标上号码1、2和3.现任取3面,它们的颜色与号码均不相同的概率是 .
11.抛物线y2=8-4x的准线方程是 ,圆心在该抛物线的顶点且与其准线相切的圆的方程是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com