
5.总体分布估计:
总体分布估计主要指两类.一类是用样本的频率分布去估计总体(的概率)分布.二类是用样本的某些数字特征(例如平均数、方差、标准差等)去估计总体的相应数字特征.
4.总体分布和样本频率分布
总体取值的_______分布规律称为总体分布.
样本频率分布_______称为样本频率分布.
3.分层抽样
当已知总体由_______的几部分组成时,为了使样本更能充分地反映总体的情况,常将总体分成几个部分,然后按照各部分所占的_______进行抽样,这种抽样叫做_______.其中所分成的各个部分叫做_______.
2.简单随机抽样
设一个总体由N个个体组成,如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时,各个个体被抽到的_______相等,就称这样的抽样为_______.
1.总体、样本、样本容量
我们要考察的对象的全体叫做_______,其中每个考察的对象叫_______.从总体中抽出的一部分个体叫做_______,样本中个体的数目叫做_______.
3.会用样本平均数估计总体期望,会用样本的方差、标准差估计总体方差、标准差.
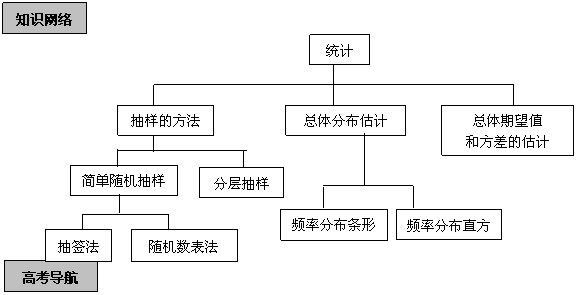
“统计”这一章,是初中数学中的“统计初步”的深化和拓展.要求主要会用随机抽样,分层抽样的方法从总体中抽取样本,并用样本频率分布估计总体分布.本章高考题以基本题(中、低档题)为主,每年只出一道填空题,常以实际问题为背景,综合考查学生应用基础知识解决实际问题的能力.高考的热点是总体分布的估计和抽样方法.知识的交汇点是排列、组合、概率与统计的解答题.
|
2.会用样本频率分布估计总体的概率分布.
1.了解随机抽样,了解分层抽样的意义.
2. 间接证明:间接证明是不同于直接证明的又一类证明方法,反证法是一种常用的间接证明方法;反证法即从 开始,经过正确的推理,说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法(归谬法).
|
例1.若 均为实数,且
均为实数,且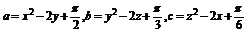 。
。
求证: 中至少有一个大于0。
中至少有一个大于0。
答案:(用反证法)
假设 都不大于0,即
都不大于0,即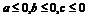 ,则有
,则有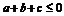 ,
,
而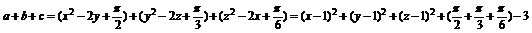 =
=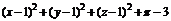
∴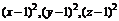 均大于或等于0,
均大于或等于0,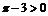 ,∴
,∴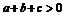 ,这与假设
,这与假设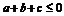 矛盾,故
矛盾,故 中至少有一个大于0。
中至少有一个大于0。
变式训练1:用反证法证明命题“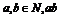 可以被5整除,那么
可以被5整除,那么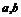 中至少有一个能被5整除。”那么假设的内容是
中至少有一个能被5整除。”那么假设的内容是
答案:a,b中没有一个能被5整除。解析:“至少有n个”的否定是“最多有n-1个”。
例2. △ABC的三个内角A、B、C成等差数列,
求证: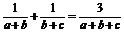 。
。
答案:证明:要证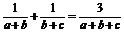 ,即需证
,即需证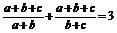 。
。
即证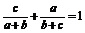 。
。
又需证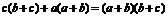 ,需证
,需证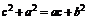
∵△ABC三个内角A、B、C成等差数列。∴B=60°。
由余弦定理,有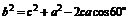 ,即
,即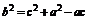 。
。
∴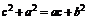 成立,命题得证。
成立,命题得证。
变式训练2:用分析法证明:若a>0,则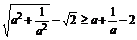 。
。
答案:证明:要证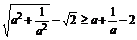 ,
,
只需证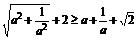 。
。
∵a>0,∴两边均大于零,因此只需证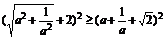
只需证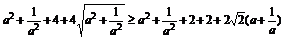 ,
,
只需证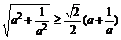 ,只需证
,只需证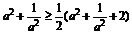 ,
,
即证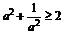 ,它显然成立。∴原不等式成立。
,它显然成立。∴原不等式成立。
例3.已知数列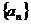 ,
,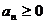 ,
,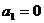 ,
,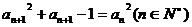 .
.
记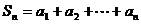 .
.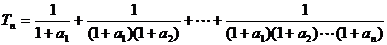 .
.
求证:当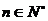 时,
时,
(1) ;
;
(2)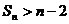 ;
;
(3)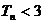 。
。
解:(1)证明:用数学归纳法证明.
①当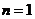 时,因为
时,因为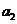 是方程
是方程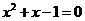 的正根,所以
的正根,所以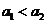 .
.
②假设当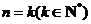 时,
时,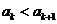 ,
,
因为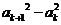
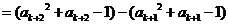
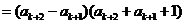 ,
,
所以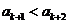 .
.
即当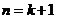 时,
时,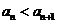 也成立.
也成立.
根据①和②,可知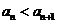 对任何
对任何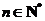 都成立.
都成立.
(2)证明:由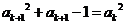 ,
,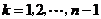 (
( ),
),
得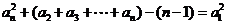 .
.
因为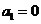 ,所以
,所以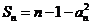 .
.
由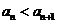 及
及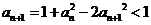 得
得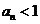 ,
,
所以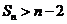 .
.
(3)证明:由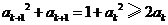 ,得
,得
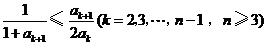
所以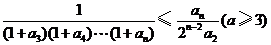 ,
,
于是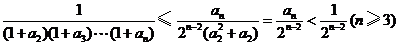 ,
,
故当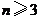 时,
时,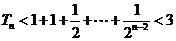 ,
,
又因为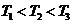 ,
,
所以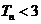 .
.
1.直接证明:直接从原命题的条件逐步推得结论成立,这种证明方法叫直接证明;
直接证明的两种基本方法--分析法和综合法
⑴ 综合法 -- ;⑵分析法 -- ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com