3．方差(1)

分别称为数据的方差和标准差，它们反映的是数据的稳定与波动，集中与离散的程度．

(2)

(3)数值较大时，可以将各数据减去一个恰当的常数a,得到

例1．某班40人随机平均分成两组，两组学生一次考试的成绩情况如下表：

求全班的平均成绩和标准差．

解：设第一组20名学生的成绩为;

第二组20名学生的成绩为,

故全班平均成绩为：

又设第一组学生的成绩的标准差为，第二组学生的成绩的标准差为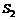，则

此处()

又设全班40名学生的标准差为S,平均成绩为故有

变式训练1：对甲乙的学习成绩进行抽样分析，各抽5门功课，得到的观测值如下：

甲：60　 80　 70　 90　 70

乙：80　 60　 70　 80　 75

问：甲乙谁的各科平均成绩好？谁的各门功课发展较平衡？

解：　 　　　　因为，．所以甲的平均成绩较好,乙的各门发展较平衡．

例2. 甲乙两台机床在相同的条件下同时生产一种零件，现在从中各抽测10个，它们的尺寸分别为(单位：mm)

甲： 10.2　 10.1　 10.9　 8.9　 9.9　 10.3　 9.7　 10　　　　　　

2．样本平均数(也称样本期望值)

(1)反映的是这组数据的平均水平．

(2)当数值较大时，可将各个数据同时减去一个适当的数，得＝,那么

(3)如果个数据中，出现次， 出现次,…, 出现次，那么：

这里

1．在统计学中，我们是用样本的数字特征来估计总体相应的数字特征的．

5．统计内容的实践性较强，其重点是如何用样本频率分布去估计总体分布，难点是对频率分布直方图的理解和应用．

第2课时　　 总体特征数的估计

4．频率分布条形图是用高度来表示概率的，而概率分布直方图是用面积来表示概率的．

3．注意以下几个概念的区别与联系：频数、频率、概率．

2．简单随机抽样是一种不放回抽样，所取的样本没有被重复抽取的情况．分层抽样，分层时不要求均分，但抽样时，要按各层中个体总数的比例在各层中抽取个体．以上两种抽样都是一种等概率抽样(即抽样方法的公平性)．这种等概率抽样包含有两层含义，其一、每次从总体中抽取一个个体时，各个个体被抽取的概率是相等的．其二、在整个抽样过程中，各个个体被抽取到的概率相等．

1．两种抽样方法的比较：

6．频率分布条形图和直方图：

两者都是用来表示总体分布估计的．其横轴都是表示总体中的个体．但纵轴的含义却截然不同．前者纵轴(矩形的高)表示频率；后者纵轴表示频率与组距的比，其相应组距上的频率等于该组距上的矩形的面积．