
21.(本小题满分18分)
设函数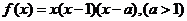
(1)求导数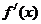 ; 并证明
; 并证明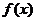 有两个不同的极值点
有两个不同的极值点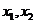 ;
;
(2) 若不等式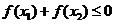 成立,求
成立,求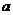 的取值范围。
的取值范围。
解:P:0<C<1,………………………………………………3分
Q: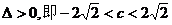 …………………………………………3分
…………………………………………3分
当P真Q假时,c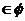 ……………………………………4分
……………………………………4分
当P假Q真时,c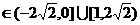 …………………………5分
…………………………5分
19(本小题满分17分)
解:(1) ………………………………………3分
………………………………………3分
所以,x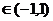 时递增,
时递增,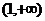 递减。………………………4分
递减。………………………4分
(2)x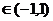 时递增,
时递增,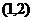 递减
递减
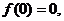
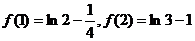 ,…………………6分
,…………………6分
所以,f(x)最大值=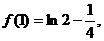 f(x)最小值=
f(x)最小值=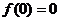 。………4分
。………4分
20、(本题满分15分)
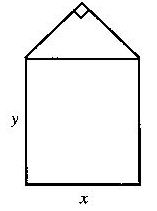
某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位:m)的矩形,上部是等腰直角三角形。 要求框架围成的总面积8cm2, 问x为多少时用料最省?
19. (本小题满分17分)
已知函数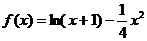
(1)讨论函数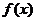 的单调区间;
的单调区间;
(2)求函数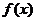 在[0,2]上的最大值和最小值。
在[0,2]上的最大值和最小值。
18.(本小题满分15分)
设 P:函数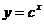 在R上单调递减.
在R上单调递减.
Q:函数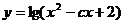 的定义域为R,如果P且Q为假命题、P或Q为真命题,求
的定义域为R,如果P且Q为假命题、P或Q为真命题,求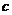 的取值范围.
的取值范围.
17.若存在常数 ,使得函数
,使得函数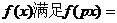
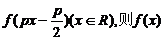 的最小正周期为
.
的最小正周期为
.
16.若函数f(x)=a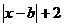 在[0,+∞)上为增函数,则实数a、b的取值范围是
.
在[0,+∞)上为增函数,则实数a、b的取值范围是
.
15.设函数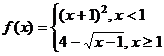 ,则使得
,则使得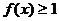 的自变量
的自变量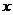 的取值范围为
.
的取值范围为
.
14.函数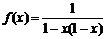 的最大值是
.
的最大值是
.
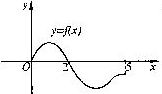
13.设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时,
f(x)的图象如右图,则不等式f(x)<0的
解是 .
12. 已知
已知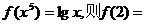 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com