
2.钠与酸溶液反应
当钠投入酸溶液中,钠首先与酸电离出的H+反应: ;当酸完全反应后,过量的钠再与水反应,故钠与酸溶液反应比钠与水反应 。
1.钠与水的反应可以概括为: 五个字来记忆。
(1)钠投入水中并浮在水面上--密度 水。
(2)钠立即跟水反应,并 ,发出嘶嘶声,产生气体。
(3)同时钠熔成一个闪亮的小球并在水面上向各方向迅速游动最后消失-- 。(4)反应后的水溶液使酚酞 --与水反应生成NaOH。
104、(上海市部分重点中学2008届高三第二次联考)已知等比数列 的首项
的首项 ,公比为
,公比为 ,其前
,其前 项和为
项和为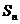
(1)求函数 的解析式;(2)解不等式
的解析式;(2)解不等式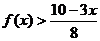 .
.
[解](1)当 时,
时, ,
,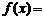
 ;…………2分
;…………2分
当 且
且 时,
时,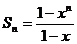 ,
,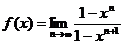 ,……………………4分
,……………………4分
若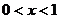 ,
, ;……………5分,若
;……………5分,若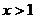 ,则
,则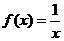 ,……………6分
,……………6分
综上, ……………………7分
……………………7分
(2)当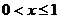 时,由
时,由 ,得
,得 ;……………………10分
;……………………10分
当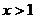 时,由
时,由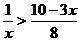 ,得
,得 或
或 。………………13分
。………………13分
综上可得原不等式的解集为 。…………………14分
。…………………14分
103、(山西大学附中2008届二月月考)在直角坐标平面上有一点列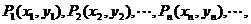 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0, ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求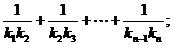
(3)设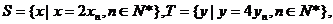 等差数列
等差数列 的任一项
的任一项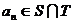 ,其中
,其中 是
是 中的最大数,
中的最大数, ,求数列
,求数列 的通项公式.
的通项公式.
解:(1)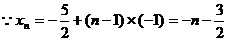 ,
,
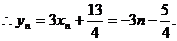

(2)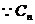 的对称轴垂直于x轴,且顶点为Pn,∴设
的对称轴垂直于x轴,且顶点为Pn,∴设 的方程为
的方程为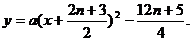
把 ,∴
,∴ 的方程为
的方程为
∵ ∴
∴
∴

= (3)
(3) ,
,
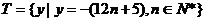
 ,
,
∴S∩T=T,T中最大数a1=-17.
设 公差为d,则a10=
公差为d,则a10=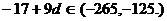
由此得 又∵
又∵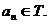
∴ ∴
∴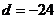 ,∴
,∴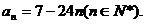
102、(山东省郓城一中2007-2008学年第一学期期末考试)已知等比数列 中,
中, 分别是某等差数列的第5项,第3项,第2项,且
分别是某等差数列的第5项,第3项,第2项,且 ,公比
,公比 ;
;
(1)求
(2)设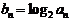 ,求数列
,求数列 的前n项和
的前n项和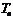 。
。
解:(Ⅰ)依题意得

(Ⅱ)

又

101、(山西省实验中学2007-2008学年度高三年级第四次月考)设等比数列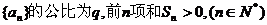 ,
,
(1)求q的取值范围;
(2)设 的大小。
的大小。
解:(1) …………1分
…………1分
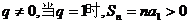 …………2分
…………2分
当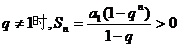 …………3分
…………3分
 …………6分
…………6分
(2)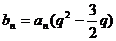 …………7分
…………7分
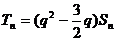 …………8分
…………8分
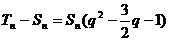 …………9分
…………9分
 …………10分
…………10分
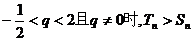 …………11分
…………11分
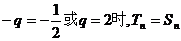 …………12分
…………12分
100、(山东省实验中学2008届高三第三次诊断性测试)设数列 的前
的前 项和为
项和为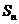 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
,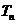 为数列
为数列 的前
的前 项和. 求证:
项和. 求证: .
.
解:(1)由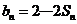 ,令
,令 ,则
,则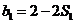 ,又
,又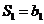 ,所以
,所以 .
.
 ,则
,则 .…………………………………2分
.…………………………………2分
当 时,由
时,由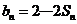 ,可得
,可得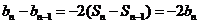 .
.
即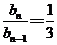 . ………3分
. ………3分
所以 是以
是以 为首项,
为首项,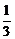 为公比的等比数列,于是
为公比的等比数列,于是 .……………4分
.……………4分
(2)数列 为等差数列,公差
为等差数列,公差 ,可得
,可得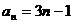 .…………6分
.…………6分
从而 .
………………………7分
.
………………………7分
∴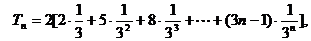
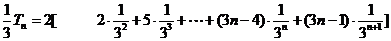
∴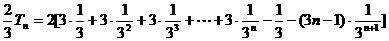 . ……………10分
. ……………10分
从而 . ………………………12分
. ………………………12分
99、(山东省聊城市2008届第一期末统考)在直角坐标平面上有一点列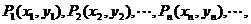 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0, ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求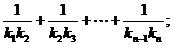
(3)设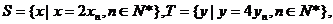 等差数列
等差数列 的任一项
的任一项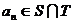 ,其中
,其中 是
是 中的最大数,
中的最大数, ,求数列
,求数列 的通项公式.
的通项公式.
解:(1)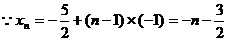
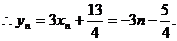
 ……………………4分
……………………4分
(2)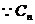 的对称轴垂直于x轴,且顶点为Pn,
的对称轴垂直于x轴,且顶点为Pn,
∴设 的方程为
的方程为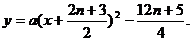
把 ,
,
∴ 的方程为
的方程为
∵ ……………………6分
……………………6分
∴
∴

= …………………………8分
…………………………8分
(3)
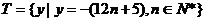

∴S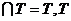 中最大数a1=-17.…………………………10分
中最大数a1=-17.…………………………10分
设 公差为d,则a10=
公差为d,则a10=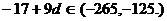
由此得
又∵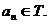
∴
∴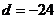
∴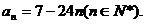 ……………………12分
……………………12分
98、(山东省济南市2008年2月高三统考)在数列 中,
中, .
.
(1)求数列 的通项;
的通项;
(2)若 对任意
对任意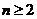 的整数恒成立,求实数
的整数恒成立,求实数 的取值范围;
的取值范围;
(3)设数列 ,
,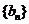 的前
的前 项和为
项和为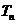 ,求证:
,求证: .
.
解:(1)将 整理得:
整理得: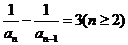 1分
1分
所以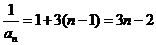 ,即
,即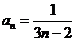 3分
3分
 时,上式也成立,所以,
时,上式也成立,所以,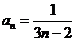 5分
5分
(2)若 恒成立,即
恒成立,即 恒成立 6分
恒成立 6分
整理得:
令
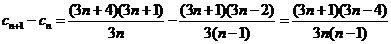 8分
8分
因为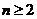 ,所以上式
,所以上式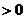 ,即
,即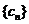 为单调递增数列,所以
为单调递增数列,所以 最小,
最小, ,
,
所以 的取值范围为
的取值范围为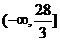 10分
10分
(3)由 ,得
,得
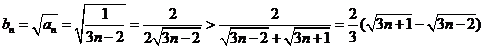
所以,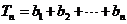

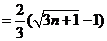 14分
14分
97、(宁夏区银川一中2008届第六次月考)等比数列{xn}的各项为不等于1的正数,数列{yn}满足 =2(a>0,且a≠1),设y3=18,
y6=12,
=2(a>0,且a≠1),设y3=18,
y6=12,
(1)证明数列{yn}是等差数列并求前多少项和最大,最大值是多少?
(2)试判断是否存在自然数M,使得当n>M时,xn>1恒成立,若存在,求出相应的M;若不存在,请说明理由
解:(1)yn=2logaxn, yn+1=2logaxn+1 yn+1 – yn=2[logaxn+1 – logaxn]=2loga
{xn}为等比数,  为定值,
所以{yn}为等差数列。
为定值,
所以{yn}为等差数列。
又因为y6- y3=3d=-6 d=-2 y1=y3-2d =22
Sn=22n+ =
- n2+23n
=
- n2+23n
故当n=11或n=12时,Sn取得最大值132。
(2) yn=22+(n-1)(-2)=2logaxn xn=a12-n>1
当a>1时,12-n>0, n<12
当0<a<1时,12-n<0 n>12,
所以当0<a<1时,存在M=12,当n>M时,xn>1恒成立。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com