
27.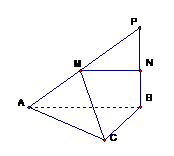 如图,在三角形⊿ABC中,∠ACB=90º,AC=b,BC=a,P是⊿ABC 所在平面外一点,PB⊥AB,M是PA的中点,AB⊥MC,求异面直MC与PB间的距离.
如图,在三角形⊿ABC中,∠ACB=90º,AC=b,BC=a,P是⊿ABC 所在平面外一点,PB⊥AB,M是PA的中点,AB⊥MC,求异面直MC与PB间的距离.
解析:作MN//AB交PB于点N.(2分)∵PB⊥AB,∴PB⊥MN。(4分)又AB⊥MC,∴MN⊥MC.(8分)MN即为异面直线MC与PB的公垂线段,(10分)其长度就是MC与PB之间的距离,
则得MN=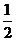 AB=
AB=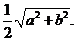
26. 在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD的中点,若AC + BD = a ,AC
在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD的中点,若AC + BD = a ,AC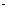 BD =b,求
BD =b,求 .
.
解析:四边形EFGH是平行四边形,…………(4分) =2
=2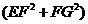 =
=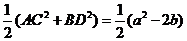
25. 在空间四边形ABCD中,E,F分别是AB,BC的中点.求证:EF和AD为异面直线.
解析:假设EF和AD在同一平面 内,…(2分),则A,B,E,F
内,…(2分),则A,B,E,F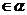 ;……(4分)又A,E
;……(4分)又A,E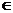 AB,∴AB
AB,∴AB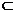
 ,∴B
,∴B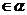 ,……(6分)同理C
,……(6分)同理C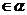 ……(8分)故A,B,C,D
……(8分)故A,B,C,D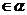 ,这与ABCD是空间四边形矛盾。∴EF和AD为异面直线.
,这与ABCD是空间四边形矛盾。∴EF和AD为异面直线.
24.设直线a上有6个点,直线b上有9个点,则这15个点,能确定_____个不同的平面.
解析: 当直线a,b共面时,可确定一个平面; 当直线a,b异面时,直线a与b上9个点可确定9个不同平面,直线b与a上6个点可确定6个不同平面,所以一点可以确定15个不同的平面.
23.OX,OY,OZ是空间交于同一点O的互相垂直的三条直
线,点P到这三条直线的距离分别为3,4,7,则OP长
为_______.
解析:在长方体OXAY-ZBPC中,OX、OY、OZ是相交的三条互相垂直的三条直线。又PZ OZ,PY
OZ,PY OY,PX
OY,PX OX,有 OX2+OZ2=49,OY2=OX2=9,
OY2+OZ2=16,
OX,有 OX2+OZ2=49,OY2=OX2=9,
OY2+OZ2=16,
得 OX2+OY2+OZ2=37,OP=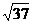 .
.
22.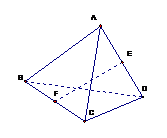
 如图,正四面体
如图,正四面体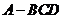 (空间四边形的四条边长及两对角线的长都相等)中,
(空间四边形的四条边长及两对角线的长都相等)中,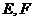 分别是棱
分别是棱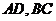 的中点, 则
的中点, 则
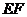 和
和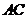 所成的角的大小是________.
所成的角的大小是________.
解析:设各棱长为2,则EF=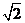 ,取AB的中点为M,
,取AB的中点为M, 即
即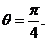
4.2米
解析:树高为AB,影长为BE,CD为树留在墙上的影高,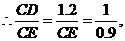 CE=
CE=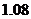 米,树影长BE=
米,树影长BE=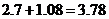 米,树高AB=
米,树高AB= BE=
BE=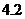 米。
米。
考生例文1
麻雀只看到了燕子的缺点--逃避严寒,而忘记了燕子所立下的种种功绩。其他的几只鸟也大抵如此。它们只注意到了别的鸟的缺点,而置优点若罔闻。这难免会出现所发出的种种错误的见解和偏激的论断。其实,燕子逃避严寒又何尝不是一种必要的、明智的选择呢?
我们待人处事也应分成两面,既要看到人或事物的缺点,更要注意发掘利用他们的优点。这就需要我们利用辩证的观点去分析问题、解决问题。燕子逃避严寒是真,但这又何尝不是求得生存的一种手段呢?我们对待问题不仅应当判断它的正误,还要辩证地找到正中之误、误中之正。正的要发扬光大,误的要摒弃杜绝。
中国有许多格言都曾论述过要辩证地看待问题的重要性。如“尺有所短,寸有所长”、“金无足赤,人无完人”等等。既然完美无缺的事物本不存在,我们就更应辩证地看待问题,找出美中不足以及不足中的可取之处来。
辩证的观点在我们的实际生活中也极为重要。例如对待一个学生,不仅要看他的成绩,还要看他的各个方面。优秀的学生如此,差的学生亦应如此。如果学习不好,德、体、美都很出色,那也就为差生不差了。又如我国的改革开放,一开始就有人抱着怀疑甚至是否定的态度。诚然,改革开放也难免混进一些渣滓,但纵观全局,辩证分析,利大于弊。所以坚持下去,终于取得了成功。
我们应用辩证的观点去分析问题、解决问题。不能因为地里长着荒草就放弃了一地的青苗。也不能只因荒原中仅存的一棵青苗而把它说成是良田。如果我们也像鸟类那样相互攻击、讥讽,岂不令智者嗤笑!对待人或事物,都应一分为二,既要看到优点又要善于发现不足,但不应以此为据,互相攻击。
简评:本文的中心词是“辩证”。不但以“辩证”为题,以“辩证”开篇,而且以“辩证”展开议论,以“辩证”阐述道理,最后“辩证”统领全文。作者巧妙地将哲学原理运用到作文中,构成了整篇文章内在的主旋律,给人一种中心明确,论点鲜明,重点突出的感觉。
请在下面三个题目中任选一个,自拟题目,写一段300字左右的赏析文章。
(1)赏析文章的抒情艺术
(2)赏析文章的细节描写
(3)赏析文章的构思艺术
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com