
22.(14分)(1)已知: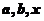 均是正数,且
均是正数,且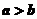 ,求证:
,求证: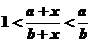 ;
;
(2)当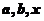 均是正数,且
均是正数,且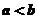 ,对真分数
,对真分数 ,给出类似上小题的结论,并予以证明;
,给出类似上小题的结论,并予以证明;
(3)证明:△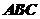 中,
中,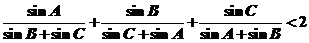 (可直接应用第(1)、(2)小题结论)
(可直接应用第(1)、(2)小题结论)
(4)自己设计一道可直接应用第(1)、(2)小题结论的不等式证明题,并写出证明过程.
21. (12分)已知关于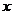 的不等式
的不等式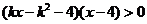 ,其中
,其中 .
.
(1)当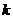 变化时,试求不等式的解集
变化时,试求不等式的解集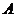 ;
;
(2)对于不等式的解集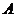 ,若满足
,若满足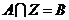 (其中
(其中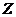 为整数集). 试探究集合
为整数集). 试探究集合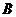 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合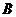 中元素个数最少的
中元素个数最少的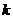 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合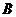 ;若不能,请说明理由.
;若不能,请说明理由.
20.(12分)
设函数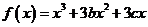 在两个极值点
在两个极值点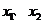 ,且
,且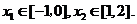
(1)求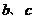 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点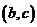 的区域;
的区域;
(2)证明: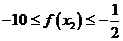
19.(12分)某种商品的成本为5元/件,开始按8元/件销售,销售量为50件,为了获取最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:销售价每上涨1元每天销售量就减少10件;而降价后,日销售量Q (件)与实际销售价x (元)满足关系
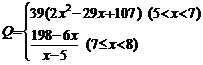
(1)求总利润(利润=销售额-成本)y(元)与实际销售价x (件)的函数关系式;
(2)试问:当实际销售价为多少元时,总利润最大.
18.(12分)已知函数 和
和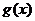 的图象关于原点对称,且
的图象关于原点对称,且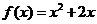 .
.
(Ⅰ)求函数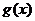 的解析式;
的解析式;
(Ⅱ)解不等式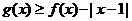 .
.
17.(12分)研究问题:“已知关于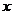 的不等式
的不等式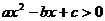 的解集为
的解集为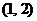 ,解关于
,解关于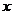 的不等式
的不等式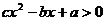 ”,有如下解法:
”,有如下解法:
解:由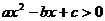
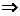
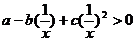 ,令
,令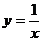 ,则
,则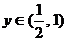 ,
,
所以不等式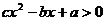 的解集为
的解集为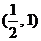 .
.
参考上述解法,已知关于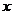 的不等式
的不等式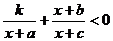 的解集为
的解集为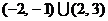 ,求关于
,求关于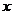 的不等式
的不等式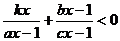 的解集.
的解集.
16. 给出下列四个命题:
①若a>b>0,c>d>0,那么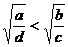 ;
;
②已知a、b、m都是正数,并且a<b,则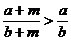 ;
;
③若a、b∈R,则a2+b2+5≥2(2a-b);
④2-3x-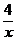 的最大值是2-4
的最大值是2-4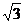 .
.
⑤原点与点(2,1)在直线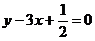 的异侧.
的异侧.
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
15.已知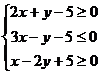 ,则z=(x+1)2+(y+1)2的取值范围是
.
,则z=(x+1)2+(y+1)2的取值范围是
.
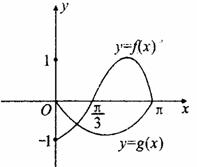 13.已知y=f(x)是偶函数,y=g(x)是奇函数,x∈[0,
13.已知y=f(x)是偶函数,y=g(x)是奇函数,x∈[0,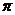 ]
]
上的图象如图,则不等式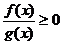 的解集是
的解集是
.
14.已知向量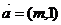 与
与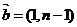 互相垂直,且点
互相垂直,且点
(m,
n)在第一象限内运动,则 的
的
最大值是 .
12. 已知函数 的定义域为[-2,
的定义域为[-2,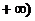 ,部分对应值如下表,
,部分对应值如下表,
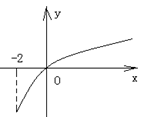
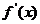 为
为 的导函数,函数
的导函数,函数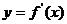 的图象如右图所示:
的图象如右图所示:
|
|
-2 |
0 |
4 |
 |
1 |
-1 |
1 |
若两正数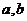 满足
满足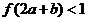 ,则
,则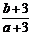 的取值范围是 ( )
的取值范围是 ( )
A.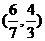 B.
B.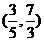 C.
C.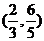 D.
D.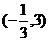
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com