
6.设f(x)定义在实数集上的周期为2的函数,且为偶函数,当x∈[0,1]时,
 ,则
,则 由小到大的顺序是____________
由小到大的顺序是____________
简答.提示:1-4.DBCB; 4.取 ;取x1=x2=-1得f(-1)=0
;取x1=x2=-1得f(-1)=0
再取x1=-1,x2=x得f(-x)=f(x); 5. 0.5; 6. 周期是2且偶函数可得

又在[0,1]上f(x)=x-2008,是增函数,且
[解答题]
5.设f(x)是R的奇函数,f(x+2)=-f(x),当0≤x≤1,时,f(x)=x,则f(7.5)=
4.(2004福建)定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则( )
A.f(sin )<f(cos
)<f(cos )
B.f(sin1)>f(cos1)
)
B.f(sin1)>f(cos1)
C.f(cos )<f(sin
)<f(sin )
D.f(cos2)>f(sin2)
)
D.f(cos2)>f(sin2)
[填空题]
3.设f(x)是R上的实函数,且满足:f(10+x)=f(10-x),f(20+x)= -f(20-x),则f(x)是( )
A.是偶函数又是周期函数 B.是偶函数但不是周期函数
C.是奇函数又是周期函数 D.是奇函数但不是周期函数
2.已知f(x)对任意的整数x都有f(x+2)=f(x-2),若f(0)=2003,则f(2004)= ( ) A.2002 B.2003 C.2004 D.2005
1.(2007石家庄质检)已知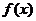 是定义在R上的偶函数,且
是定义在R上的偶函数,且 恒成立,当
恒成立,当 时,
时, ,则当
,则当 时,函数
时,函数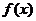 的解析式为( )
的解析式为( )
A. B.
B. C.
C. D.
D. 
2.抽象函数处理方法,主要是“赋值法”,通常是抓住函数特性,利用变量代换解题。要能灵活驾驭函数性质及概念的本质。也常联系具体的函数模型可以简便地找到解题思路,及解题突破口。
同步练习 2.11 抽象函数
[选择题]
1.抽象函数一般是函数的一些特性,由这些特性讨论函数的单调性、奇偶性、周期性及图象的对称性,或是求函数值、解析式等。
[例1]已知函数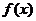 对一切
对一切 ,都有
,都有 ,求证:
,求证:
(1)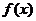 是奇函数;(2)若f(x)的图象关于直线x=1对称,则f(x)恒等于0.
是奇函数;(2)若f(x)的图象关于直线x=1对称,则f(x)恒等于0.
解:(1)在 中,
中,
令 ,得
,得 ,
,
令 ,得
,得 ,∴
,∴ ,
,
∴ ,即
,即 , ∴
, ∴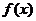 是奇函数
是奇函数
(2)f(x)是奇函数,则f(-x)=-f(x).且f(0)=0
图象关于直线x=1对称,即点(x,y),(2-x,y)同在曲线上,有f(2-x)=f(x),
且f(2)=f(0)=0 又已知f(x+y)=f(x)+f(y)
∴f(x)= f(2-x)=f(2)+f(-x)=f(2)-f(x) 2f(x)=f(2)=0即f(x)≡0.
2f(x)=f(2)=0即f(x)≡0.
方法提炼:1.赋值法.赋值的目的要明确,本题就是要凑出f(0),f (-x)与f(x)的关系;2.领会函数式变换的依据、目的和策略的灵活性。
[例2]已知函数f(x)的定义域是x≠0的一切实数,对定义域内的任意x1,x2都有 ,且当
,且当 时
时 ,
,
(1)求证:f(x)是偶函数; (2)f(x)在(0,+∞)上是增函数;
(3)解不等式
解:(1)令 ,得
,得 ,∴
,∴ ,
,
令 ,得
,得 ,
,
∴ ,
,
∴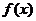 是偶函数
是偶函数
(2)设 ,则
,则


∵ ,∴
,∴ ,∴
,∴
 ,
,
即 ,∴
,∴
∴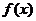 在
在 上是增函数
上是增函数
(3) ,∴
,∴ ,
,
∵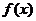 是偶函数
是偶函数
∴不等式 可化为
可化为 ,
,
又∵函数在 上是增函数,
上是增函数,
∴0≠ ,解得:
,解得: ,
,
即不等式的解集为
[例3] 定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)·f(b).
(1)求证:f(0)=1;
(2)求证:对任意的x∈R,恒有f(x)>0;
(3)求证:f(x)是R上的增函数;
(4)若f(x)·f(2x-x2)>1,求x的取值范围.
(1)证明:令a=b=0,则f(0)=f 2(0).
又f(0)≠0,∴f(0)=1.
(2)证明:当x<0时,-x>0,
∴f(0)=f(x)·f(-x)=1.
∴f(-x)= >0.又x≥0时f(x)≥1>0,
>0.又x≥0时f(x)≥1>0,
∴x∈R时,恒有f(x)>0.
(3)证明:设x1<x2,则x2-x1>0.
∴f(x2)=f(x2-x1+x1)=f(x2-x1)·f(x1).
∵x2-x1>0,∴f(x2-x1)>1.
又f(x1)>0,∴f(x2-x1)·f(x1)>f(x1).
∴f(x2)>f(x1).∴f(x)是R上的增函数.
(4)解:由f(x)·f(2x-x2)>1,f(0)=1得f(3x-x2)>f(0).又f(x)是R上的增函数, ∴3x-x2>0.∴0<x<3.
关键点注:解本题的关键是灵活应用题目条件,尤其是(3)中“f(x2)=f[(x2-x1)+x1]”是证明单调性的关键,这里体现了向条件化归的策略.
[例4]已知f(x)是定义在R上的函数,且f(x+2)(1-f(x))=1+f(x).
(1)求证:f(x)是周期函数; (2)若 ,试求f(2001),f(2005)的值。
,试求f(2001),f(2005)的值。
解:




解题要点 用活条件 ,
,
[研究.欣赏] 函数f(x)对一切实数x,y均有f(x+y)-f(y)=(x+2y+1)x成立,且f(1)=0, (1)求 的值; (2)对任意的
的值; (2)对任意的 ,
, ,都有f(x1)+2<logax2成立时,求a的取值范围.
,都有f(x1)+2<logax2成立时,求a的取值范围.
解:(1)由已知等式 ,
,
令 ,
, 得
得 ,
,
又∵ ,∴
,∴ .
.
(2)由 ,
,
令 得
得 ,
,
由(1)知 ,∴
,∴ .∵
.∵ ,
,
∴ 在
在 上单调递增,
上单调递增,
∴ .
.
要使任意 ,
, 都有
都有 成立,必有
成立,必有 都成立.
都成立.
当 时,
时, ,显然不成立.
,显然不成立.
当 时,
时, ,解得
,解得
∴ 的取值范围是
的取值范围是 .
.
方法提炼 怎样赋值?需要明确目标,细心研究,反复试验;(2)小题中实质是不等式恒成立问题.
6.由已知: =2,∴
=2,∴ ,原式=16
,原式=16
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com