
7.已知元素原子的下列结构或性质,能确定其在周期表中位置的是:
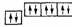 A.某元素原子的第二电子层电子排布图为
A.某元素原子的第二电子层电子排布图为
B.某元素的在某种化合物中化合价为+4
C.某元素的原子最外层上电子数为6
D.某元素原子的外围电子排布式为5s25p1
6.某原子的最外层电子排布为nsnnp2n+1,则该元素在周期表中的位置为:
A.第二周期,ⅢA族 B.第二周期,ⅦA族
C.第五周期,ⅡA族 D.第七周期,ⅡA族
5.某原子的一种激发态为1s22s12p1,则该元素在周期表中的位置为:
A.第二周期,ⅠA族 B.第二周期,ⅡA族
C.第一周期,ⅠA族 D.第一周期,ⅡA族
4.根据下列微粒的最外层电子排布,能确定形成该微粒的元素在周期表中的准确位置的是:
A.1s2 B.3s23p1 C.2s22p6 D.ns2np3
3.第四周期元素原子中未成对的电子数最多可达:
A.4个 B.5个 C.6个 D.7个
2.几种微粒具有相同的核电荷数,则它们:
A.一定属于同种元素 B.一定互为同位素
C.可能属于不同的分子、原子或离子 D.核外电子数一定相等
1.简单原子的原子结构可用
右图表示方法形象地表示:
其中●表示质子或电子,
○表示中子,则下列有关
①②③地叙述正确的是:
A.①②③互为同位素 B.①②③互为同素异形体
C.①②③是三种化学性质不同的粒子 D.①②③具有相同的质量数
22.(本小题满分14分)
已知不等式 为大于2的整数,
为大于2的整数,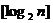 表示不超过
表示不超过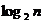 的最大整数. 设数列
的最大整数. 设数列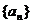 的各项为正,且满足
的各项为正,且满足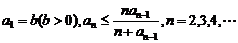
(Ⅰ)证明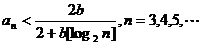
(Ⅱ)猜测数列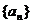 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)试确定一个正整数N,使得当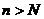 时,对任意b>0,都有
时,对任意b>0,都有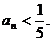
本小题主要考查数列、极限及不等式的综合应用以及归纳递推的思想.
(Ⅰ)证法1:∵当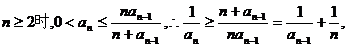
即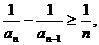
于是有 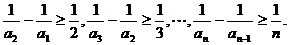
所有不等式两边相加可得 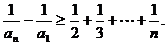
由已知不等式知,当n≥3时有,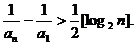
∵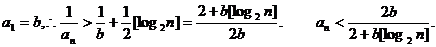
证法2:设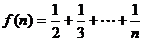 ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式
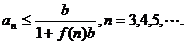
(i)当n=3时, 由 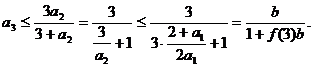
知不等式成立.
(ii)假设当n=k(k≥3)时,不等式成立,即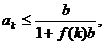
则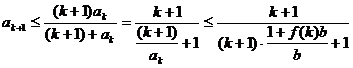
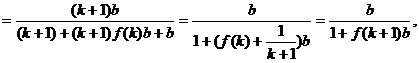
即当n=k+1时,不等式也成立.
由(i)、(ii)知,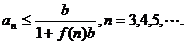
又由已知不等式得 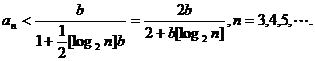
(Ⅱ)有极限,且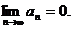
(Ⅲ)∵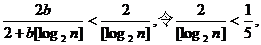
则有
故取N=1024,可使当n>N时,都有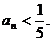
21.(本小题满分12分)
设A、B是椭圆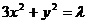 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定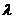 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的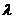 ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
(此题不要求在答题卡上画图)
本小题主要考查直线、圆和椭圆等平面解析几何的基础知识以及推理运算能力和综合解决问题的能力.
(Ⅰ)解法1:依题意,可设直线AB的方程为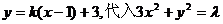 ,整理得
,整理得 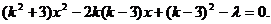 ①
①
设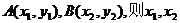 是方程①的两个不同的根,
是方程①的两个不同的根,
∴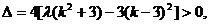 ②
②
且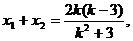 由N(1,3)是线段AB的中点,得
由N(1,3)是线段AB的中点,得
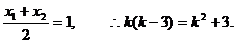
解得k=-1,代入②得,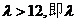 的取值范围是(12,+∞).
的取值范围是(12,+∞).
于是,直线AB的方程为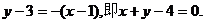
解法2:设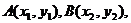 则有
则有
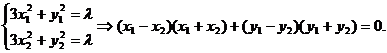
依题意,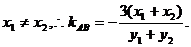
∵N(1,3)是AB的中点, ∴
又由N(1,3)在椭圆内,∴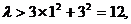
∴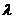 的取值范围是(12,+∞).
的取值范围是(12,+∞).
直线AB的方程为y-3=-(x-1),即x+y-4=0.
(Ⅱ)解法1:∵CD垂直平分AB,∴直线CD的方程为y-3=x-1,即x-y+2=0,
代入椭圆方程,整理得 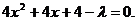
又设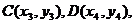 CD的中点为
CD的中点为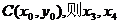 是方程③的两根,
是方程③的两根,
∴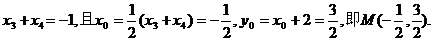
于是由弦长公式可得 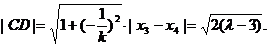 ④
④
将直线AB的方程x+y-4=0,代入椭圆方程得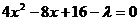 ⑤
⑤
同理可得 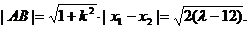 ⑥
⑥
∵当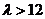 时,
时,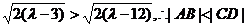
假设存在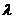 >12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
>12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
点M到直线AB的距离为 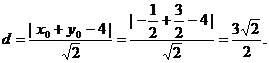 ⑦
⑦
于是,由④、⑥、⑦式和勾股定理可得
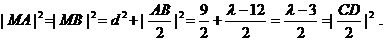
故当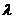 >12时,A、B、C、D四点匀在以M为圆心,
>12时,A、B、C、D四点匀在以M为圆心,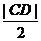 为半径的圆上.
为半径的圆上.
(注:上述解法中最后一步可按如下解法获得:)
A、B、C、D共圆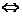 △ACD为直角三角形,A为直角
△ACD为直角三角形,A为直角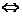 |AN|2=|CN|·|DN|,
|AN|2=|CN|·|DN|,
即
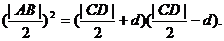 ⑧
⑧
由⑥式知,⑧式左边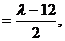
由④和⑦知,⑧式右边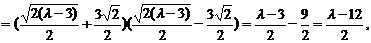
∴⑧式成立,即A、B、C、D四点共圆.
解法2:由(Ⅱ)解法1及λ>12,
∵CD垂直平分AB, ∴直线CD方程为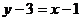 ,代入椭圆方程,整理得
,代入椭圆方程,整理得
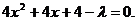 ③
③
将直线AB的方程x+y-4=0,代入椭圆方程,整理得
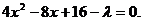 ⑤
⑤
解③和⑤式可得 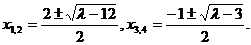
不妨设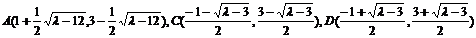
∴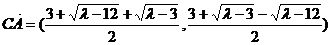
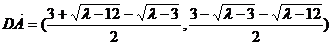
计算可得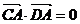 ,∴A在以CD为直径的圆上.
,∴A在以CD为直径的圆上.
又B为A关于CD的对称点,∴A、B、C、D四点共圆.
(注:也可用勾股定理证明AC⊥AD)
2.湖北理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com