
2.当a>b>c时,下列不等式恒成立的是 ( )
A.ab>ac B.a|c|>b|c|
C.|ab|<|bc| D.(a-b)|c-b|>0
解析:∵a>b>c,∴(a-b)>0.
又∵|c-b|>0,∴选D.
答案:D
1.(2009·四川高考)已知a,b,c,d为实数,且c>d,则“a>b”是“a-c>b-d”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
解析:由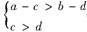 ⇒a>b;而当a=c=2,b=d=1时,满足
⇒a>b;而当a=c=2,b=d=1时,满足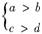 ,但a-c>b-d不成立,所以“a>b”是“a-c>b-d”的必要而不充分条件,选B.
,但a-c>b-d不成立,所以“a>b”是“a-c>b-d”的必要而不充分条件,选B.
答案:B
22.(14分)已知函数f(x)=Asin(ωx+φ)+B(A>0,0<ω<2,|φ|<)的一系列对应值如下表:
|
x |
- |
|
|
|
|
|
|
|
y |
-1 |
1 |
3 |
1 |
-1 |
1 |
3 |
(1)根据表格提供的数据求函数y=f(x)的解析式;
(2)若对任意的实数a,函数y=f(kx)(k>0),x∈
(a,a+]的图象与直线y=1有且仅有两个不同的交点,又当x∈[0,]时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
解:(1)依题意,T==2[-(-)],∴ω=1.
又,解得
f()=2sin(+φ)+1=3,|φ|<,解得φ=-
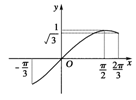
图3
∴f(x)=2sin(x-)+1为所求.
(2)由已知条件可知,函数y=f(kx)=2sin(kx-)+1的周期为,又k>0,∴k=3
令t=3x-,∵x∈[0,],
∴t=3x-∈[-,]
而y=sint在[-,]上单调递增,在[,]上单调递减,且sin=sin=(如图3),
∴sint=s在[-,]上有两个不同的解的充要条件是s∈[,1),
方程f(x)=m恰有两个不同的解的充要条件是m∈
[+1,3).
21.(12分)(2009·江西九校联考)已知函数f(x)=m·n,其中m=(sinωx+cosωx,cosωx),n=(cosωx-sinωx,2sinωx),其中ω>0,若f(x)相邻两对称轴间的距离不小于.
(1)求ω的取值范围;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,a=,b+c=3,当ω最大时,f(A)=1,求△ABC的面积.
解:(1)f(x)=cos2ωx-sin2ωx+2sinωxcosωx=cos2ωx+sin2ωx=2sin(2ωx+).
∵ω>0,∴函数f(x)的周期T==,
由题意可知≥,即T≥π,
解得0<ω≤1,即ω的取值范围是{ω|0<ω≤1}.
(2)由(1)可知ω的最大值为1,
∴f(x)=2sin(2x+),
∵f(A)=1,∴sin(2A+)=.
而<2A+<π,
∴2A+=π,∴A=.
由余弦定理知cosA=,
∴b2+c2-bc=3,又b+c=3,
联立解得或,
∴S△ABC=bcsinA=.
20.(12分)(2009·江苏南京模拟)已知函数f(x)=2cos2x+
2sinxcosx.
(1)求函数f(x)在[-,]上的值域;
(2)在△ABC中,若f(C)=2,2sinB=cos(A-C)-cos(A+C),求tanA的值.
解:(1)f(x)=2cos2x+2sinxcosx=1+cos2x+sin2x
=2sin(2x+)+1,
∵-≤x≤,
∴-≤2x+≤,-≤sin(2x+)≤1.
∴0≤2sin(2x+)+1≤3.
∴f(x)在区间[-,]上的值域为[0,3].
(2)f(C)=2sin(2C+)+1=2,sin(2C+)=,
∵0<C<π,∴<2C+<2π+.
∴2C+=,即C=.
∵2sinB=cos(A-C)-cos(A+C)=2sinAsinC,
∴sin(A+C)=sinAsinC,sinAcosC+cosAsinC=sinAsinC,
tanA===.
19.(12分)已知向量m=(cos,cos),n=(cos,sin),且x∈[0,π],令函数f(x)=2am·n+b.
(1)当a=1时,求f(x)的递增区间;
(2)当a<0时,f(x)的值域是[3,4],求a,b.
解:(1)m·n=cos2+sincos=+sinx.
∴f(x)=a(sinx+cosx)+a+b=asin(x+)+a+b.
当a=1时,f(x)=sin(x+)+b+1.
∵x∈[0,π],∴x+∈[,π],由≤x+≤,得0≤x≤.∴f(x)的递增区间是[0,].
(2)当a<0时,f(x)=asin(x+)+a+b.
易知sin(x+)∈[-,1],
∴f(x)∈[(+1)a+b,b].
则,∴.
18.(12分)(2009·广西南宁模拟)已知函数f(x)=+asin2x在x=时取得最大值.
(1)求函数f(x)的定义域;
(2)求实数a的值.
解:(1)∵cos2x≠0,∴2x≠kπ+(k∈Z),
∴f(x)的定义域为{x|x≠kπ+,k∈Z}.
(2)∵f(x)=+asin2x=2sin2x+(1-cos2x),
∴f(x)=2sin2x-cos2x+≤+.
∵在x=时,f(x)取得最大值,则
2sin-cos=,
∴3-=,求得a=-4.
17.(12分)求的值.
解:=
=
==
==.
16.给出下列命题:①若{an}成等比数列,Sn是前n项和,则S4,S8-S4,S12-S8成等比数列;②已知函数y=2sin(ωx+θ)为偶函数(0<θ<π),其图象与直线y=2的交点的横坐标为x1、x2,若|x1-x2|的最小值为π,则ω的值为2,θ的值为;③函数y=f(x)的图象与直线x=a至多有一个交点;④函数y=2sin(2x-)的图象的一个对称点是(,0);
其中正确命题的序号是__________.(把你认为正确命题的序号都填上)
解析:当q=-1时,S4=S8=S12=0,∴①错.
∵y=2sin(ωx+θ)为偶函数,0<θ<π,
∴2sin(-ωx+θ)=2sin(ωx+θ),∴cosθ=0.∴θ=.
∵|x2-x1|的最小值为π,周期为2π,ω=±1.∴②错.
答案:③④
15.已知函数f(x)=sin(x-)+cos(x-),g(x)=f(-x),直线x=m与f(x)和g(x)的图象分别交于M,N两点,则|MN|的最大值为__________.
解析:f(x)=2sin(x-+)=2sinx,
g(x)=f(-x)=·2sin(-x)=2cosx,
f(x)-g(x)=2sinx-2cosx=4sin(x-)
故|MN|的最大值为4.
答案:4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com