12．(2009·郑州二模)已知命题P：不等式lg[x(1－x)+1]>0的解集为{x|0<x<1}；命题Q：在三角形ABC中，∠A>∠B是cos²(+)<cos²(+)成立的必要而非充分条件，则(　)

A．P真Q假　 　　　　　　　　　　　　　 B．P且Q为真

C．P且Q为假　 　　　　　　　　　　　 D．P假Q真

解析：依题意，由lg[x(1－x)+1]>0得x(1－x)+1>1，∴x－x²>0，解得0<x<1，所以命题P正确；在三角形ABC中，∠A>∠B⇔sinA>sinB⇔－cos(+A)>－cos(+B)⇔

－2cos²(+)+1>－2cos²(+)+1⇔cos²(+)<cos²(+)，所以命题Q是假命题，选择A.

答案：A

11．(2010·东北三校一模)设函数f(x)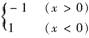＝，则(a≠b)的值为　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．a　 　　　　　　　　　　　　　　　　　　　 B．b

C．a、b中较小的数　 　　　　　　　 D．a、b中较大的数

解析：对a－b进行讨论，当a－b>0时，f(a－b)＝－1，＝＝b；当a－b<0时，f(a－b)＝1，＝＝a，所以上式的值为a、b中较小的数．选C.

答案：C

10．如果函数f(x)＝a^x(a^x－3a²－1)(a>0且a≠1)在区间[0，+∞)上是增函数，那么实数a的取值范围是　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(0，]　 　　　　　　　　　　　　　　　 B．[，1)

C．(1，]　 　　　　　　　　　　　　　　 D．(，+∞)

解析：令a^x＝t，则y＝t²－(3a²+1)·t，

对称轴＝－＝≥.

①当0<a<1时，则0<a^x<1.

欲使x∈[0，+∞)递增，只需≥1，

即3a²+1≥2，即a²≥.

∴a≥或a≤－(舍去)．

②当a>1时，a^x>1不成立，故选B.

答案：B

9．(2010·西安八校联考)已知正整数a、b满足4a+b＝30，则使得+取得最小值的有序数对(a，b)是　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(5,10)　 　　　　　　　　　　　　　　　 B．(6,6)

C．(7,2)　 　　　　　　　　　　　　　　　　 D．(10,5)

解析：依题意得+＝(+)(4a+b)＝(4+++1)≥，当且仅当＝时取最小值，即b＝2a，再由4a+b＝30，解得.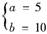

答案：A

8．(2009·成都一诊)下列四个命题中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．若a，b∈R，则|a|－|b|<|a+b|

B．若a，b∈R，则|a－b|<|a|+|b|

C．若实数a，b满足|a－b|＝|a|+|b|，则ab≤0

D．若实数a，b满足|a|－|b|<|a+b|，则ab<0

解析：对于A，当a＝2，b＝0时，|a|－|b|＝|a+b|，因此A不正确；对于B，当a＝2，b＝0时，|a－b|＝|a|+|b|，因此B不正确；对于D，当a＝0，b＝2时，满足|a|－|b|<|a+b|，但ab＝0，因此D不正确．综上，选C.

答案：C

7．(2009·西城抽样)设a、b∈R，且b(a+b+1)<0，b(a+b－1)<0，则　　　　　　 (　)

A．a>1　 　　　　　　　　　　　　　　　　　 B．a<－1

C．－1<a<0　 　　　　　　　　　　　　　 D．|a|>1

解析：在坐标平面aOb中作出不等式组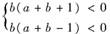

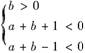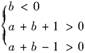即①与②表示的平面区域，结合图形观察可知，该平面区域内的任意一点(a，b)的横坐标都满足|a|>1，因此选D.

答案：D

6．已知a>0，b>0，a、b的等差中项为，且α＝a+，β＝b+，则α+β的最小值是(　)

A．3　 　　　　　　　　　　　　　　　　　　　 B．4

C．5　 　　　　　　　　 　　　　　　　　　　 D．6

解析：由已知条件知a+b＝1，∴1＝a+b≥2.

∴ab≤.∴α+β＝1+≥5(当且仅当a＝b时取等号)．

答案：C

5．不等式≤0的解集为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．{－1}　 　　　　　　　　　　　　　　　 B．[－1,1]

C．[－1,1)　 　　　　　　　　　　　　　　 D．(－1,1]

解析：由≤0可得，

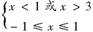∴，即得x∈[－1,1)．

答案：C

4．(2010·武汉调研)若实数a、b∈(0,1)，且满足(1－a)b>，则a、b的大小关系是(　)

A．a<b　 　　　　　　　　　　　　　　　　　 B．a≤b

C．a>b　 　　　　　　　　　　　　　　　　　 D．a≥b

解析：∵a、b∈(0,1)，∴1－a>0，又(1－a)b>，∴<()²，<，b－a>0，选择A.

答案：A

3．若a>1,0<b<1，则下列不等式中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．a^b<1　 　　　　　　　　　　　　　　　　 B．b^a>1

C．log_ab<0　 　　　　 　　　　　　　　　　 D．log_ba>0

解析：a>1,0<b<1，则log_ab<log_a1＝0.

答案：C